Relação de Euler

A relação de Euler é uma fórmula fundamental na topologia de poliedros e superfícies, que estabelece uma conexão entre o número de vértices (V), arestas (A) e faces (F) de um poliedro convexo. A fórmula é expressa como:

          V – A + F = 2

 Esta relação é incrível porque se aplica a qualquer poliedro convexo, não importa a forma ou complexidade. Vamos entender cada um dos componentes:

1. Vértices (V): Os pontos onde as arestas de um poliedro se encontram.
2. Arestas (A): As linhas que conectam os vértices.
3. Faces (F): As superfícies planas que formam as fronteiras do poliedro.

Sólidos	Vértices	Faces	Arestas	Relação de Euler V – A + F = 2
Cubo	8	6	12	8 – 12 + 6 = 2
Paralelepípedo	8	6	12	8 – 12 + 6 = 2
Pirâmide quadrangular	4	4	6	4 – 6 + 4 = 2
Pirâmide hexagonal	5	5	8	5 – 8 + 5 = 2
Pirâmide retangular	7	7	12	7 – 12 + 7 = 2
Pirâmide triangular	5	5	8	5 – 8 + 5 = 2
Prisma triangular	6	5	9	6 – 9 + 5 = 2
Prisma hexagonal	12	8	18	12 – 18 + 8 = 2
Tetraedro	4	4	6	4 – 6 + 4 = 2

Relação entre o número de arestas e lados de um poliedro

Para encontrar o número de aresta podemos calcular o número total de lados e dividir o resultado por dois, visto que cada aresta (A) é a intersecção de dois lados (L):

Exemplos de Aplicação da Relação de Euler:

• Cubo: Um cubo tem 8 vértices, 12 arestas e 6 faces. Aplicando a relação de Euler:

      V – A + F = 2
      8 – 12 + 6 = 2
      – 4 + 6 = 2

• Tetraedro: Um tetraedro tem 4 vértices, 6 arestas e 4 faces. Aplicando a relação de Euler:

      V – A + F = 2
      4 – 6 + 4 = 2
      – 2 + 4 = 2

Exercícios

1 – Determine o número de faces de um sólido que apresenta 10 arestas e 6 vértices.

Resolução:

V = 6
A = 10
F = ?

V – A + F = 2

6 – 10 + F = 2
– 4 + F = 2
F = 2 + 4 = 6
F = 6 faces

2 – (FAAP/SP) Num poliedro convexo, o número de arestas excede o número de vértices em 6 unidades. Calcule o número de faces.

Resolução:
• De acordo com o enunciado, temos:

A = V + 6

• Usando a Relação de Euler e substituindo A de acordo com a igualdade acima:

F = ?
V – A + F = 2

V – (V + 6) + F = 2
V – V – 6 + F = 2
– 6 + F = 2
F = 2 + 6 = 8
F = 8 faces.

3 – Um poliedro possui 16 faces e 18 vértices. Qual é o número de arestas desse poliedro?
a) 16         b) 18          c) 32         d) 34         e) 40

Resolução:
V = 18

A = ?

F = 16

V – A + F = 2

18 – A + 16 = 2

32 – A = 2

34 – 2 = A

A = 32 arestas.

4 – O número de faces de um poliedro convexo que possui 34 arestas é igual ao número de vértices. Quantas faces possui esse poliedro?

a) 18          b) 20          c) 36          d) 34          e) 19

Resolução:

• De acordo com o enunciado, temos:

F = V    e    A = 34

• Usando a Relação de Euler e substituindo F de acordo com a igualdade acima:

F = ?
V – A + F = 2

V – A + V = 2

V – 34 + V = 2

V + V = 2 + 34

2V = 36

V = 36:2

V = 18

• Como F = V:

F = 18 faces

5 – Um poliedro convexo, o número de vértices é 5 e o de aresta é 10. Qual é o número de faces?

Resolução:

V = 5

A = 10

F = ?

V – A + F = 2

5 – 10 + F = 2

– 5 + F = 2

F = 2 + 5

F= 7 faces.

6 – Em um poliedro convexo de 20 arestas, o número de faces é igual ao número de vértices. Quantas faces tem esse poliedro?

Resolução:

• De acordo com o enunciado, temos:

F = V    e    A = 20

• Usando a Relação de Euler e substituindo F de acordo com a igualdade acima:

F = ?

V – A + F = 2

V – A + V = 2

V – 20 + V = 2

V + V = 2 + 20

2V = 22

V = 22:2

V = 11

• Como F = V:      F = 11 faces.   

7 – O número de faces de um poliedro convexo de 22 arestas é igual ao número de vértices. Então, qual o número de faces do poliedro?

Resolução:
• De acordo com o enunciado, temos:
F = V    e    A = 22
• Usando a Relação de Euler e substituindo F de acordo com a igualdade acima:
F = ?
V – A + F = 2
V – A + V = 2
V – 22 + V = 2
V + V = 2 + 22

2V = 24
V = 24:2
V = 12
Como F = V:
F = 12 faces

 8 – Um poliedro convexo tem 9 faces e 16 arestas. Determine o número total de vértices desse poliedro.

Resolução:

V = ?
A = 16
F = 9
V – A + F = 2
V – 16 + 9 = 2
 V – 7 = 2
V = 2 + 7
V = 9 vértices

 9 – Num poliedro convexo, o número de arestas é 12 unidades maior que o número de vértices. Calcule o número de faces desse poliedro.

Resolução:

• De acordo com o enunciado, temos:

A = V + 12

• Usando a Relação de Euler e substituindo A de acordo com a igualdade acima:

F = ?

V – A + F = 2

V – (V + 12) + F = 2

V – V – 12 + F = 2

– 12 + F = 2

F = 2 + 12

F = 14 faces

10 – O número de arestas de arestas de um octaedro convexo é o dobro do número de vértices. Quantas arestas possui esse poliedro?

Resolução:

• De acordo com o enunciado, temos:

A = 2V   e    F = 8 (octaedro)

• Usando a Relação de Euler e substituindo A de acordo com a igualdade acima:

A = ?

V – A + F = 2

V – 2V + F = 2

V – 2V + 8 = 2

– V + 8 = 2

– V = 2 – 8

– V = 2 – 8

– V = – 6     ⋅( – 1)

V = 6

• Como A = 2V:

A = 2⋅6

A = 12 arestas.

11 – Utilizando a relação de Euler, marque o número de arestas de um dodecaedro convexo, sabendo que esse sólido possui 12 faces e 20 vértices.

a) (   ) 30    b) (   ) 32    c) (   ) 40    d) (   ) 42

Resolução:

A = ?

V = 20

F = 12

V – A + F = 2

20 – A + 12 = 2

– A + 32 = 2

– A = 2 – 32

– A = – 30    ⋅( – 1)

A = 30 arestas.

12 – Num poliedro convexo, o número de faces é 20 e o número de vértices é 12. Qual é o número de arestas desse poliedro?

Resolução:

A = ?
F = 20

V = 12
V – A + F = 2
12 – A + 20 = 2
32 – A = 2
– A = 2 – 32
– A = – 30    ⋅( – 1)
A = 30 arestas.

13 – Um poliedro convexo é constituído por três faces triangulares, cinco quadrangulares e sete pentagonais. Quantas arestas e quantos vértices possui esse poliedro?

Resolução:

A = ?
V = ?

F = 3 + 5 + 7 = 15

L = 9 + 20 + 35 = 64

• Na fórmula abaixo vamos fazer: Lados (L) e Aresta (A):

V – A + F = 2

V – 32 + 15 = 2

V – 17 = 2     V = 2 + 17 = 19

• Resposta: Esse poliedro possui 32 arestas e 19 vértices. 

14 – Determine o número de vértices de um poliedro que tem três faces triangulares, uma face quadrangular, uma pentagonal e duas hexagonais.

Resolução:

V = ?

F = 3 + 1 + 1 + 2 = 7

L = 9 + 4 + 5 +12 = 30

• Na fórmula abaixo vamos fazer: Lados (L) e Aresta (A):

V – A + F = 2

V – 15 + 7 = 2
V – 8 = 2     

V = 2 + 8 = 10
Resposta: Esse poliedro possui 10 vértices.      

15 – Um poliedro convexo tem 5 faces triangulares, 6 faces quadrangulares e 3 faces pentagonais. Calcule o número de faces, arestas e vértices desse poliedro.

Resolução:

F = ?       A = ?       V = ?

F = 5 + 6 + 3 = 14

L = 15 + 24 + 15 = 54

• Na fórmula abaixo vamos fazer: Lados (L) e Aresta (A):

V – A + F = 2
V – 27 + 14 = 2
V – 13 = 2     

V = 2 + 13 = 15

• Resposta: Esse poliedro possui 14 faces, 27 arestas e 15 vértices. 

16 – Um poliedro convexo é formado por 80 faces triangulares e 12 pentagonais. O número de arestas desse poliedro é:

      a) 150     b) 180     c) 190     d) 200     e) 240 

      Resolução:   

      A = ?

     

L = 240 + 60 = 300

• Na fórmula abaixo vamos fazer: Lados (L) e Aresta (A):

Resposta: Letra A 

17 – Determine o número de arestas e o número de vértices de um poliedro convexo com 6 faces quadrangulares e 4 faces triangulares.

A = ?

V = ?

F = 6 + 4 = 10

L = 24 + 12 = 36

• Na fórmula abaixo vamos fazer: Lados (L) e Aresta (A):

V – A + F = 2

V – 18 + 10 = 2

V – 8 = 2     V = 2 + 8 = 10

• Resposta: Esse poliedro possui 18 arestas e 10 vértices. 

18 – Um poliedro convexo apresenta 1 face hexagonal e 6 faces triangulares. Quantos vértices tem esse poliedro?

V = ?

F = 1 + 6 = 7

L = 6 + 18 = 24

• Na fórmula abaixo vamos fazer: Lados (L) e Aresta (A):

V – A + F = 2

V – 12 + 7 = 2

V – 5 = 2     V = 2 + 5 = 7

• Resposta: Esse poliedro possui 7 vértices. 

19 – Determine o número de vértices de um poliedro convexo que tem 3 faces triangulares, 1 face quadrangular, 1 face pentagonal e 2 faces hexagonais.

V = ?

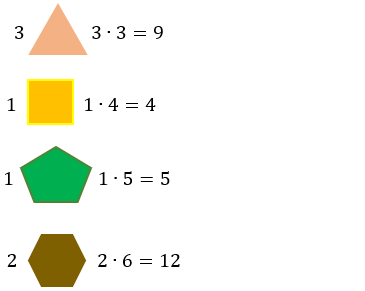
F = 3 + 1 + 1 + 2 = 7

L = 9 + 4 + 5 + 12 = 30

• Na fórmula abaixo vamos fazer: Lados (L) e Aresta (A):

V – A + F = 2

V – 15 + 7 = 2

V – 8 = 2     V = 2 + 8 = 10

• Resposta: Esse poliedro possui 10 vértices.