Inequação quociente do primeiro grau

As inequações quociente do primeiro grau envolvem uma fração onde o numerador e o

denominador são expressões lineares (do primeiro grau). Estas inequações podem ser

expressas nas formas:

         

Onde a, b, c e d são constantes, x é a variável, e os operadores de comparação:

           (<, >, ≤, ≥).

Passos para resolver uma inequação quociente do primeiro grau:

1. Encontrar os pontos críticos: Determine os valores de x que fazem o numerador e o denominador iguais a zero. Estes pontos são importantes porque dividem a reta numérica em intervalos onde a inequação pode mudar de sinal.
2. Analisar os intervalos: Divida a reta numérica nos intervalos definidos pelos pontos críticos. Em cada intervalo, determine o sinal da expressão quociente.
3. Determinar as regiões onde a inequação é verdadeira: Com base na análise dos intervalos, identifique quais intervalos satisfazem a desigualdade dada.
4. Considerar as exclusões de domínio: Se cx + d = 0 em algum ponto crítico, esse ponto deve ser excluído do conjunto solução, pois a expressão quociente não está definida quando o denominador é zero.

  Exemplo:

  Resolver a inequação:

• Pontos críticos:
  Numerador: 2x − 3 = 0 → x =1.5
  Denominador: x + 1 = 0 → x = −1
• Intervalos:
  (− ∞, −1)
  (−1, 1.5)
  (1.5, ∞)
• Análise dos sinais nos intervalos:
  x < − 1: O numerador e o denominador são negativos, logo a fração é positiva.
  − 1 < x < 1.5: O numerador é negativo e o denominador é positivo, logo a fração é negativa.
  x > 1.5: O numerador e o denominador são positivos, logo a fração é positiva.
• Solução:
  x < −1 ou x > 1.5

• Portanto, a solução da inequação é x ∈ (− ∞, −1) ∪ (1.5, ∞).

      Exercícios

1 – Resolva a inequação:

Resolução:

• Numerador:

x – 2 = 0

x = 2

a = 1 > 0

• Função crescente:

• Denominador(Condição de existência):

x + 3 ≠ 0

x ≠ – 3

• Denominador(Raiz):

x + 3 = 0
x = – 3

a = 1 > 0

• Função crescente:

Solução: x < −  3 ou x >2.
Portanto, a solução da inequação é x ∈ (− ∞, − 3) ∪ (2, ∞).                     

2 – Resolva a inequação:

Resolução:

• Numerador:

• Função crescente: 

• Denominador(Condição de existência):

• Denominador(Raiz):
 
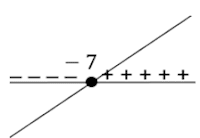
• Função decrescente:

• Solução: − 7 ≤ x < 2

3 – Resolva a inequação de 1º grau:

Resolução:

• O mínimo múltiplo comum entre x + 1  e 1 é x + 1:

• Numerador:

• Função decrescente:

• Denominador(Condição de existência):

• Denominador (Raiz):

• Função crescente:

• Solução: 

x <  – 1

ou