Lei dos Senos e dos Cossenos

A lei dos senos é uma ferramenta poderosa em trigonometria que relaciona os comprimentos dos lados de um triângulo qualquer com os senos de seus ângulos opostos. Ela é especialmente útil para resolver triângulos oblíquos, ou seja, triângulos que não têm um ângulo reto.

A fórmula da lei dos senos é expressa da seguinte maneira:

Onde:

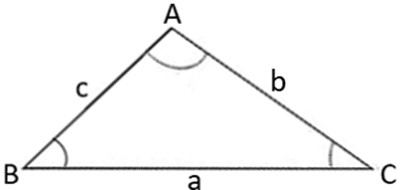
• a, b e c são os comprimentos dos lados do triângulo.

• A, B e C são os ângulos opostos a esses lados.

A lei dos cossenos, também conhecida como teorema de Al-Kashi, é uma fórmula fundamental na trigonometria que relaciona os comprimentos dos lados de um triângulo com o cosseno de um de seus ângulos. Esta lei é particularmente útil para resolver triângulos que não são retângulos, onde a lei dos senos pode não ser suficiente. Por não estar restrita ao triângulo retângulo, a lei dos cossenos pode ser entendida como uma generalização do teorema de Pitágoras.

Em qualquer triângulo, o quadrado de um dos lados é igual à soma dos quadrados dos outros dois lados, menos o dobro do produto desses dois lados pelo cosseno do ângulo formado entre eles. Ou seja: Ao contrário da lei dos senos, a lei dos cossenos torna-se importante na obtenção de elementos do triângulo, conhecendo mais lados do que ângulos. Sua aplicação é válida para todos os tipos de triângulo, mas no triângulo retângulo temos uma ocorrência interessante. Considerando o triângulo retângulo a seguir, ao aplicar a lei dos cossenos obtemos: c2 = a2 + b2 – 2∙a∙b∙cos ϒ c2 = a2 + b2 – 2∙a∙b∙cos 90o c2 = a2 + b2 – 0 c2 = a2 + b2 Assim, podemos verificar que o teorema de Pitágoras pode ser aplicado como sendo uma variação da lei dos cossenos. Resumindo: Dois lados e um ângulo: Aplicar a lei dos cossenos. Dois ângulos e um lado: Utilizar a lei dos senos. Exercícios 1 – Utilizando a lei dos cossenos, determine o valor do segmento x no triângulo a seguir: a² = b² + c² – 2∙b∙c∙cosϒ 7² = x² + 3² – 2∙3∙x∙cos 60º 49 = x² + 9 – 6∙x∙0,5 49 = x² + 9 – 3x x² – 3x – 40 = 0 Aplicando o método resolutivo da equação do 2º grau, temos: x = 8 e x = – 5, por se tratar de medidas descartamos x = – 5 e utilizamos x = 8. Então o valor de x no triângulo é 8 cm. 2 – Em um triângulo ABC, temos as seguintes medidas: AB = 6 cm, AC = 5 cm e BC = 7 cm. Determine a medida do ângulo A. Vamos construir o triângulo com as medidas fornecidas no exercício. Aplicando a lei dos cossenos a = 7, b = 6 e c = 5 7² = 6² + 5² – 2∙6∙5∙cos A 49 = 36 + 25 – 60∙cos A 49 – 36 – 25 = – 60∙cos A – 12 = – 60∙cos A 12 = 60∙cos A 12/60 = cos A cos A = 0,2 O ângulo que possui cosseno com valor aproximado de 0,2 mede 78º. 3 – Calcule a medida da maior diagonal do paralelogramo da figura a seguir, utilizando a lei dos cossenos. cos 120º = – cos(180º – 120º) = – cos 60º = – 0,5 x² = 5² + 10² – 2∙5∙10∙(–cos 60º) x² = 25 + 100 – 100∙(–0,5) x² = 125 + 50 x² = 175 Como raiz quadrada de sete é aproximadamente igual a 2,6: x = 5 . 2,6 x = 13,2 cm