Equações do 4º grau

A forma geral de uma equação do 4º grau é 𝑎x⁴ + 𝑏x³ + 𝑐x² + 𝑑𝑥 + 𝑒 = 0, onde 𝑎 ≠ 0.

Resolução

Existem alguns métodos para a resolução de equações do 4º grau. Aqui vamos usar o método de aspa dupla.

O método de aspa dupla é um método de fatoração de polinômios, utilizado para polinômios de quarto grau. 

Para aplicar o método, deve-se: 

1. Decompor o primeiro e o último termo do polinômio em dois fatores

2. Formar uma aspa simples com os fatores obtidos

3. Realizar os produtos indicados pelas aspas

4. Subtrair o resultado obtido do terceiro termo do polinômio

5. Utilizar o resultado da divisão para substituir o terceiro termo do polinômio

6. Aplicar o método de aspa dupla com os três primeiros termos do novo polinômio

7. Os fatores do polinômio original serão os elementos horizontais das aspas

 Exemplos: Resolver as equações do 4º grau, usando o método de aspa dupla.

x² – 2x + 5 = 0

ou

x² – 2x + 2 = 0

Para:

x² – 2x + 5 = 0

a = 1,   b = – 2   e    c = 5

Para:

x² – 2x + 2 = 0

a = 1,   b = – 2   e    c = 2

Solução:

2x² – 5x – 3 = 0

ou

x² + x – 2 = 0

Para:

2x² – 5x – 3 = 0

a = 2,   b = – 5   e    c = – 3 

Para:

x² + x – 2 = 0

a = 1,   b = 1   e    c = – 2

Solução:

x² + 4x + 1 = 0

ou

 x² + 3x + 1 = 0

Para:

x² + 4x + 1 = 0

a = 1,   b = 4   e    c = 1

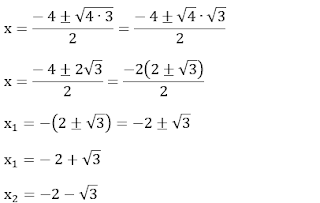
Para:

x² + 3x + 1 = 0

a = 1,   b = 3   e    c = 1  

Solução:

Exercícios

1 - Resolva as equações do 4º grau completas: 

a) 6x⁴ + 5x³ + 14x² + 6x + 5 = 0

Resolução:

3x² + x + 5 = 0

ou

 2x² + x + 1 = 0

Para:

3x² + x + 5 = 0

a = 3,   b = 1   e    c = 5

Para:

2x² + x + 1 = 0

a = 2,   b = 1   e    c = 1  

Solução:

b) 2x⁴ – 5x³ + 14x² – 10x + 3 = 0

Resolução:

2x² – 3x + 1 = 0

ou

 x² – x + 3 = 0

Para:

2x² – 3x + 1 = 0

a = 2, b = – 3  e  c = 1 

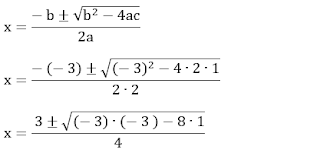
Para:

x² – x + 3 = 0

a = 1, b = – 1  e  c = 3 

Solução:

c) x⁴ – 6x³ + 14x² – 16x + 8 = 0

Resolução:

 – x² + 4x – 4 = 0

ou

– x² + 2x – 2 = 0

Para:

 – x² + 4x  – 4 = 0

a = – 1, b = 4  e  c = – 4

Para:

– x² + 2x  – 2 = 0

a = – 1, b = 2  e  c = – 2

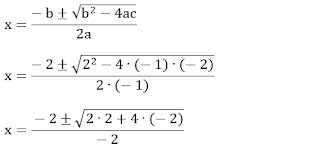
Solução:

2 - Resolva a equação do 4º grau completa 2x⁴ + x³ – 6x² + x + 2 = 0.

Resolução:

Fazendo:

Substituindo em:

ou

ou

Solução:

3 - Resolva a equação do 4º grau incompleta x⁴ – 25x² + 144 = 0.

Resolução:

Fatorando o número 144:

x + 3 = 0 ⇒ x = – 3
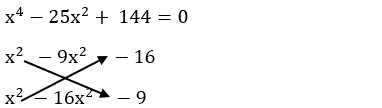
ou
x – 3 = 0 ⇒ x = 3
ou
x + 4 = 0 ⇒ x = – 4
ou
x – 4 = 0 ⇒ x = 4
Solução: {– 3, 3, – 4, 4}