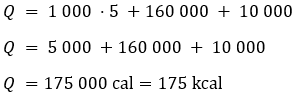As mudanças de fases são transformações que ocorrem quando uma substância muda de um estado físico para outro, como sólido, líquido ou gasoso. Esse estudo é fundamental na física e na química, pois ajuda a entender o comportamento das substâncias sob diferentes condições de temperatura e pressão.
Aqui estão os principais tipos de mudanças de fases:
Fusão: É a transformação de um sólido em líquido. Isso ocorre quando a temperatura de um sólido é elevada ao ponto de derreter. Exemplo: gelo derretendo em água.
Solidificação: É o processo inverso da fusão, onde um líquido se transforma em sólido quando a temperatura diminui. Exemplo: água se transformando em gelo.
Vaporização: É a transformação de um líquido em gás. Isso pode ocorrer de duas maneiras:
Evaporação: Quando a vaporização acontece na superfície do líquido, geralmente a temperaturas abaixo do ponto de ebulição.
Ebulição: Quando a vaporização ocorre em todo o volume do líquido, a uma temperatura específica chamada ponto de ebulição.
Condensação: É o processo inverso da vaporização, onde um gás se transforma em líquido. Exemplo: vapor d'água se transformando em gotas de água.
Sublimação: É a transformação direta de um sólido em gás, sem passar pela fase líquida. Exemplo: gelo seco (dióxido de carbono sólido) sublimando em dióxido de carbono gasoso.
Ressublimação: É o processo inverso da sublimação, onde um gás se transforma diretamente em sólido. Exemplo: formação de gelo a partir do vapor d'água em temperaturas muito baixas.

Essas mudanças de fases são governadas por princípios de termodinâmica e envolvem trocas de energia na forma de calor. Entender essas transformações é crucial para várias aplicações, desde processos industriais até fenômenos naturais.
Exercícios
1 - (Colégio Naval) Analise a tabela abaixo, considerando os pontos de fusão (PF) e ebulição (PE), a 1 atm de pressão, das substâncias a seguir.
|
Substância |
PF (°C) |
PE (°C) |
|
Cloro |
– 101,0 |
– 34,6 |
|
Flúor |
– 219,6 |
– 188,1 |
|
Bromo |
– 7,2 |
58,8 |
|
Mercúrio |
– 38,8 |
356,6 |
|
Iodo |
113,5 |
184 |
Sendo assim, é correto afirmar que, a 50 °C, encontram-se no estado líquido:
b) cloro e iodo.
c) flúor e bromo.
d) bromo e mercúrio.
e) mercúrio e iodo.
2 - (FGV) O conhecimento das propriedades físico-químicas das substâncias é muito útil para avaliar condições adequadas para a sua armazenagem e transporte.
Considere os dados das três substâncias seguintes:
Substância Ponto de fusão (°C) Ponto de ebulição (°C)
II – Flúor –220 –188
III – Césio 28 678
b) sólido, gasoso e gasoso.
c) sólido, líquido e líquido.
d) líquido, gasoso e líquido.
e) líquido, líquido e gasoso.

Pela análise do gráfico, observa-se que o álcool hidratado, a 85 ºC e 1 atm, se encontra no estado __________ e a temperatura da mistura durante a fusão __________.
Assinale a
alternativa que preenche, correta e respectivamente, as lacunas do texto.
b) gasoso – varia
c) líquido – varia
d) gasoso – permanece constante
e) líquido – permanece constante
4 - (UCS) O
diagrama de fases da água, representado abaixo, permite avaliar o estado físico
de uma amostra de água em função da pressão e da temperatura às quais está
submetida.

Com base no
diagrama de fases da água, considere as afirmativas abaixo.
I. A patinação no gelo ocorre, pois a pressão que a lâmina dos patins exerce sobre o gelo provoca a fusão da água, permitindo o deslizamento.
II. A
utilização da panela de pressão acelera o cozimento dos alimentos, pois
possibilita o aumento da temperatura de ebulição da água.
III. A água apresenta menor temperatura de ebulição em Caxias do Sul - RS, comparada a uma cidade localizada no nível do mar, onde a pressão atmosférica é maior.
Das
afirmativas acima, pode-se dizer que
a)
apenas I está correta.
b)
apenas II está correta.
c)
apenas I e III estão corretas.
d)
apenas II e III estão corretas.
e)
I, II e III estão corretas.
Dados: Calor específico do gelo = 0,5 cal/g °C; calor latente de fusão do gelo = 80 cal/g
a) 150. b) 155. c) 165. d) 170. e) 175.
2 - Alternativa A.
Estanho Flúor Césio
Sólido Gasoso Líquido

I. A patinação
no gelo ocorre, pois a pressão que a lâmina dos patins exerce sobre o gelo
provoca a fusão da água, permitindo o deslizamento.
II. A
utilização da panela de pressão acelera o cozimento dos alimentos, pois
possibilita o aumento da temperatura de ebulição da água.
III. A água apresenta menor temperatura de ebulição em Caxias do Sul - RS, comparada a uma cidade localizada no nível do mar, onde a pressão atmosférica é maior
5 - Resolução: