Lei dos senos

A lei dos senos é uma ferramenta poderosa em trigonometria que relaciona os comprimentos dos lados de um triângulo qualquer com os senos de seus ângulos opostos. Ela é especialmente útil para resolver triângulos oblíquos, ou seja, triângulos que não têm um ângulo reto.

A fórmula da lei dos senos é expressa da seguinte maneira:

Onde:

• a, b e c são os comprimentos dos lados do triângulo.

• A, B e C são os ângulos opostos a esses lados.

Exemplo: Calcule a medida x no  triângulo abaixo.

Resolução:

• Lado a = 7 cm

• Lado b = x?

• Ângulo A = 30°

• Ângulo B = 45°

x ≅ 9,898 cm

Exercícios

1 – (Mackenzie – SP) Três ilhas A, B e C aparecem num mapa em escala 1:10000, como na figura. Das alternativas, a que melhor aproxima a distância entre as ilhas A e B é:

          

a) 2,3 km
b) 2,1 km
c) 1,9 km
d) 1,4 km
e) 1,7 km

Resolução:

• Cálculo da medida do ângulo C:

• A escala 1:10000 significa que 1 cm no papel, corresponde a 10000 cm no real.

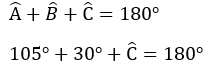
km	hm	dam	m	dm	cm	mm
0,	1	0	0	0	0

2 – (Unifor-CE) Sabe-se que em todo triângulo a medida de cada lado é diretamente proporcional ao seno do ângulo oposto ao lado. Usando essa informação, conclui-se que a medida do lado AB do triângulo representado abaixo é:

Resolução:

• Racionalizando o denominador da fração:

3 – Determine a medida x no triângulo ABC abaixo. 

Resolução:

• Usando a lei dos senos:

• Multiplicando cruzado:

4 – No triângulo a seguir, qual é a medida do segmento AC, destacada pela letra x, dado que essas medidas estão em centímetros?

Resolução:

• Primeiramente vamos calcular a medida do ângulo B:

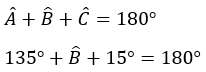
• Em segundo lugar, calcular valor do seno de 135°:

• Multiplicando cruzado:

5 – (Unicamp-SP) Qual é o valor do lado AC do triângulo?

          

Resolução:

AC = ?

• Primeiramente calcular o sen 105°, usando a propriedade dos senos:

sen 105° = sen(60° + 45°)

sen 105° = sen 60°⋅ cos 45° + cos 60°⋅ sen 45°

• Multiplicando os dois membros da equação por 4: