Os determinantes são funções matemáticas que associam a cada matriz quadrada um número real ou complexo, importante em várias áreas da matemática, como álgebra linear, geometria e cálculo. Eles desempenham um papel fundamental na solução de sistemas lineares, no cálculo de inversas de matrizes e na análise de transformações lineares.
1 - Definição de Determinante:- Para uma matriz 2x2, o determinante é calculado como:

- Para uma matriz 3x3 ou maior, o cálculo envolve somas e produtos mais complexos, frequentemente utilizando a regra de Sarrus para 3x3 e cofatores para matrizes maiores.
- Comutatividade: O determinante de uma matriz transposta é igual ao determinante da matriz original.
- Multiplicatividade: O determinante do produto de duas matrizes é igual ao produto dos determinantes dessas matrizes.
- Determinante da Matriz Identidade: O determinante de uma matriz identidade de qualquer ordem é 1.
- Linha ou Coluna de Zeros: Se uma linha ou coluna de uma matriz é composta apenas de zeros, seu determinante é zero.
- Troca de Linhas: Trocar duas linhas de uma matriz altera o sinal do determinante.
- Multiplicação por Escalar: Multiplicar uma linha de uma matriz por um escalar k multiplica o determinante por k.
- Sistemas Lineares: Usado para resolver sistemas de equações lineares pelo método de Cramer.
- Inversas de Matrizes: Uma matriz quadrada A é invertível se, e somente se, seu determinante não for zero. A inversa é dada por:
Onde adj(A) é a matriz adjunta:
- Transformações Lineares: Determinantes podem ser usados para entender a escala de transformação linear e o volume de paralelogramos ou paralelipípedos definidos por vetores.
- Regra de Sarrus: Aplicável para matrizes 3x3.
- Expansão por Cofatores: Um método geral para matrizes de qualquer ordem, onde o determinante é expresso em termos de determinantes menores (menores complementares).
Exercícios
1 – Calcule o determinante da matriz A.



2 – Encontre o valor de x, para que o
determinante da matriz A, seja igual a 5.

Resolução:




3 – (PUC-CAMP) Sejam as matrizes A, B e C:
a) – 4 b) – 2 c) 0 d) 1 e) 5
Resolução:




4 - (PUC – RS) O determinante da matriz M é:

Resolução:






5 – Considerando as matrizes abaixo,
calcule o determinante de A・B.

a) 64 b) 8 c) 0 d) – 8 e)
– 64




Sabendo que x = detA, y = detB e z = detC, onde "det" é o determinante de uma matriz, o valor de (x ⋅ z)y é:
a) 1000
b) 27
c) 1
d) – 27
e) – 1 000

(x⋅z)y = (x⋅z)0 = 1















Usando a fórmula de Bhaskara:


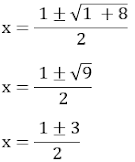

Nenhum comentário:
Postar um comentário