Equações do 3º grau

As equações do 3º grau, também conhecidas como equações cúbicas, são polinômios de grau três e têm a forma geral:

        ax³ + bx² + cx + d = 0

        Onde a, b, c e d são coeficientes reais (ou complexos), e a ≠ 0.

Conceitos e métodos importantes para o estudo das equações cúbicas:

1. Forma Geral e Reduzida:

• A forma geral de uma equação cúbica é a mencionada acima.
• Pode-se transformá-la em uma forma reduzida (sem o termo quadrático) através de uma mudança de variável, simplificando a resolução.

      2. Método de Cardano:

• Girolamo Cardano desenvolveu um método para resolver equações cúbicas no século XVI. Esse método envolve uma série de substituições e manipulações algébricas que permitem expressar as raízes da equação em termos dos coeficientes.

          ax³ + bx² + cx + d = 0

         Substituindo na equação:

         

         

          

          

           Dividindo toda equação por a:

                                 

         

           

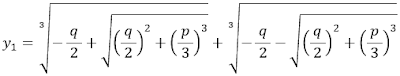
• Então, para a equação reduzida y³ + py + q = 0, as raízes podem ser encontradas utilizando a fórmula de Cardano, que envolve a solução de uma equação quadrática auxiliar.

          

          

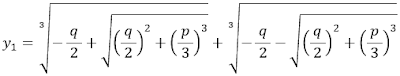
3. Discriminante:

• O discriminante de uma equação cúbica fornece informações sobre a natureza das raízes da equação (reais e distintas, reais e coincidentes, ou complexas).
• O discriminante Δ (delta) para uma equação cúbica ax³ + bx² + cx + d = 0 pode ser calculado usando a fórmula:

         

      Interpretação do discriminante

• Se Δ = 0, a equação tem uma raiz múltipla 
• Se Δ > 0, a equação tem três raízes reais distintas 
• Se Δ < 0, a equação tem um par de raízes complexas 

      4.     Raízes Reais e Complexas:

• Uma equação cúbica sempre tem pelo menos uma raiz real, já que um polinômio de grau ímpar tem pelo menos uma interseção com o eixo x.
• As outras duas raízes podem ser reais ou complexas, dependendo dos coeficientes e do discriminante.

            5.     Fatoração e Teorema do Resto:

• Se uma raiz real r for conhecida, a equação cúbica pode ser fatorada como:

         a(x − r)(x² + mx + n) = 0. 

• O Teorema do Resto pode ser usado para encontrar raízes inteiras ou racionais, ajudando na fatoração e na simplificação da equação.

     6.     Relações de Girard

• Soma das raízes: 

          

• Produto das raízes:

        

• Soma dos produtos das raízes dois a dois:

        

    Exemplos:

1 -  Resolver a equação x³ – 3x² + 12x + 16 = 0.

Resolução:

a = 1 e b = – 3

x = y + 1

Substituindo x = y + 1 em:

x³ – 3x² + 12x + 16 = 0

(y + 1)³ – 3(y + 1)² +12(y + 1) + 16 = 0

y³ + 3⋅y²⋅1 + 3⋅y⋅1² + 1³ – 3(y² +2⋅y⋅1 + 1²) +12y + 12 + 16 = 0

y³ + 3y² + 3y + 1 – 3y² – 6y – 3 + 12y + 28 = 0

y³ + 9y + 26 = 0

p = 9 e q = 26

Substituindo p e q em:

Substituindo:  

y₁ = 1 + (– 3) = 1 – 3

y₁ = – 2

Substituindo y₁ em:

x₁ = y₁ + 1

x₁ = – 2 + 1

x₁ = – 1

Usando o dispositivo prático de Briot-Ruffini para encontrar as demais raízes:

x³ – 3x² +12x + 16 = 0

Coeficientes da equação: 1, – 3,  12 e 16

Raiz:  x₁ = – 1

– 1⋅1 + (– 3) = – 1 – 3 = – 4

– 1⋅(– 4) + 12 = 4 + 12 = 16

– 1⋅16 + 16 =  – 16 + 16 = 0 

           Coeficientes       Resto

           do quociente

Q(x) = x² – 4x + 16 e R(x) = 0

x² – 4x + 16 = 0

Usando a fórmula de Bhaskara:

a = 1,    b = – 4    e    c = 16

Solução:

2 - Encontre a raiz real da equação de 3º grau x³ + 6x² – 12x + 8 = 0.

Resolução:

• Fazendo:

a = 1   e   b = 6

x = y – 2

• Substituindo x = y – 2 na equação:

• Usando os produtos notáveis:

e

• Teremos:

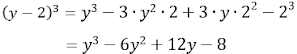
• Fazendo p = – 24 e q = 48:

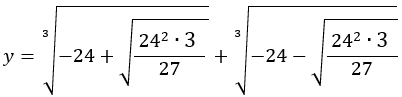
• Como x = y – 2:

• Colocando – 2 em evidência:

Resolução por fatoração:

1 - Resolva a equação do 3º grau x³ + 3x² – 6x – 18 = 0.

Resolução:

 x³ + 3x² – 6x – 18 = 0

x²⋅(x + 3) – 6⋅(x + 3) = 0

(x + 3)⋅( x² – 6) = 0

∴ x + 3 = 0  ⇾  x = – 3

ou

x² – 6 = 0  ⇾  x² = 6  

• Solução:

2 – Encontre as raízes da equação do 3º grau x³ + 2x² – x – 2 = 0.

Resolução:

x³ + 2x² – x – 2 = 0

x²⋅(x + 2) – 1⋅(x + 2) = 0

(x + 2)⋅(x² – 1) = 0

∴ x + 2 = 0  ⇾   x = – 2

ou

x² – 1 = 0  ⇾   x² = 1 

• Solução: {– 2, – 1, 1}

3 – Determine as raízes da equação do 3º grau x³ – 4x² – 10 x + 40 = 0.

x³ – 4x² – 10 x + 40 = 0

x²⋅(x – 4) – 10⋅(x – 4) = 0

(x – 4)⋅(x² – 10) = 0

∴ x – 4 = 0  ⇾   x = 4

ou

x² – 10 = 0  ⇾ x² = 10 

• Solução:

4 – Resolva em IR a equação do 3º grau 2x³ + 3x² – 18x – 27 = 0.

Resolução:

2x³ + 3x² – 18x – 27 = 0

• Reorganizando a equação:

2x³ – 18x + 3x² – 27 = 0

• Fatorando:

2x⋅(x² – 9) +3⋅(x² – 9) = 0

(x² – 9)⋅(2x – 3) = 0

• Solução:

5 – Quais são os valores de x que resolve a equação x³ – 36x = 0?

a) 6, – 6

b) 0, 6, – 6

c) 0, 6

d) 1, 2, 3

e) –1, 1

Resolução:

x⋅(x² – 36) = 0

∴  x = 0

ou

x² – 36 = 0  ⇾  x² = 36 

• Solução: {0, 6, – 6}  

6 – Encontre as raízes da equação do 3º grau x³ + x² – 12 = 0.

Resolução:

x³ + x² – 12 = 0

x³ + x² – 8 –  4 = 0

x³ + x² – 2⋅2⋅2 –  2⋅2 = 0

x³ + x² – 2³ – 2² = 0 

x³ – 2³ + x² – 2² = 0

• Fatorando: diferença de dois cubos e diferença de dois quadrados:

• Substituindo em:

x³ – 2³ + x² – 2² = 0

(x – 2)⋅( x² + 2x + 4)+ (x+2)⋅(x – 2) = 0

• Colocando (x – 2) em evidência:

(x – 2)⋅( x² + 2x + 4)+ (x + 2)⋅(x – 2) = 0

(x – 2)⋅[( x² + 2x + 4) + (x + 2)] = 0

(x – 2)⋅[( x² + 2x + 4)+ (x + 2)] = 0

(x – 2)⋅( x² + 2x + 4 + x + 2) = 0

(x – 2)⋅( x² + 3x + 6) = 0

∴ x – 2 = 0   ⇾   x = 2

ou

x² + 3x + 6 = 0

• Usando a fórmula de Bhaskara:

• Fazendo:

Solução:

7 – Resolva a equação do 3º grau x³ – 3x + 2 = 0.

Resolução:

x³ – 3x + 2 = 0

• Escrevendo – 3x = – x – 2x:

x³ – x – 2x + 2 = 0

x(x² –1) –  2(x – 1) = 0

• Usando o produto notável:

x⋅(x + 1)⋅(x –1) –  2⋅(x – 1) = 0

• Colocando x – 1 em evidência:

(x – 1)⋅[x(x + 1) – 2] = 0

(x – 1)⋅(x² + x – 2) = 0

∴ x – 1 = 0  ⇾   x = 1

ou

x² + x – 2 = 0

• Usando a fórmula de Bhaskara:

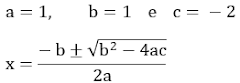
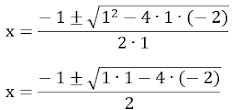
• Solução: {1, – 2}

8 – Resolva a equação 7^x +7^2x +7^3x = 14, com x ∈ IR.

Resolução:

7^x +7^2x +7^3x = 14

7^x +(7^x)² +(7^x)³ = 14

• Fazendo 7^x = z:

z + z² + z³ = 14

z + z² + z³ – 14 = 0

• Fazendo 14 = 2 + 4 + 8 = 2 +2² + 2³:

z + z² + z³ – (2 + 4 + 8) = 0

z – 2 + z² – 4 + z³ – 8 = 0

z – 2 + z² – 2² + z³ – 2³ = 0

(z – 2) + (z² – 2²) + (z³ – 2³) = 0

• Usando as fatorações de polinômios:

e

(z – 2) + (z + 2)⋅(z – 2) + (z – 2)⋅(z² +z⋅2 + 2²) = 0

1⋅(z – 2) + (z + 2)⋅ (z – 2) + (z – 2)⋅(z² + 2z + 4) = 0

• Colocando z – 2 em evidência:

(z – 2)⋅[1+ (z + 2) + (z² + 2z + 4)] = 0

(z – 2)⋅(1+ z + 2 + z² + 2z + 4) = 0

(z – 2)⋅( z² + 3z + 7) = 0

z – 2 = 0  ⇒ z = 2

e

z² + 3z + 7 = 0

• Usando a fórmula de Bhaskara:

• Como z₁ e z₂ são números complexos, vamos usar apenas z = 2 real:

• Aplicando logaritmo nos dois membros da equação:

log 7^x = log 2

x⋅log 7 = log 2

• Usando a expressão de mudança de base:

• Logo:

9 – Resolva a equação abaixo, para x > 0:

Resolução:

• Fazendo:

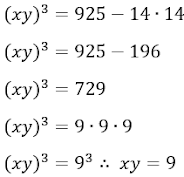
• Usando a fatoração de polinômios:

e

• Fazendo x – y = t:

• Calculando o valor do discriminante da equação de 2° grau:

Δ＜0 (Não convém)

• Substituindo t = – 1 em (4):

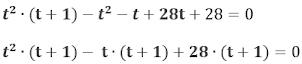
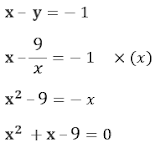
• Usando a fórmula de Bhaskara:

• Como x₂ ＜ 0, (Não convém).

• Solução:

10 – Calcule o valor de “n” na equação:

Resolução:

• Trocando as ordens dos expoentes:

• Substituindo 3ⁿ por m:

• Usando as regras de fatoração:

e

• Teremos:

• Colocando (m – 3) em evidência:

• Como:

• Calculando logaritmo nos dois membros da equação:

• Usando a propriedade:

• Dividindo os dois membros da equação por log 3:

• Usando a propriedade:

• Solução:

11 – Resolva a equação de 3º grau:

Resolução:

• Trocando as ordens dos expoentes: 

• Substituindo 3^x por m:

• Usando as regras de fatoração:

e

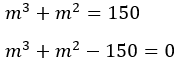
• Teremos:

• Colocando (m – 5) em evidência:

ou

• Como:

• Calculando logaritmo nos dois membros da equação:

• Usando a propriedade:

• Dividindo os dois membros da equação por log 3:

• Usando a propriedade:

• Calculando logaritmo nos dois membros da equação:

• Usando a propriedade:

• Dividindo os dois membros da equação por log 3:

• Usando a propriedade:

• Solução:

12 –  Resolva a equação 2^x + 2^3x  = 10.

2^x + 2^3x  = 10

2^x + (2^x)³  = 10

• Fazendo 2^x = y:

y + y³ = 10

y + y³ – (2 + 8) = 0

y + y³ – 2 – 8 = 0

y – 2 + y³ – 8 = 0

y – 2 + y³ – 2⋅2⋅2 = 0

(y – 2) + (y³ – 2³) = 0

y³ – 2³ = (y – 2)⋅( y² + y2 + 2²)

             = (y – 2)⋅( y² + 2y + 4)

• Substituindo em:

(y – 2) + (y³ – 2³) = 0

(y – 2) + (y – 2)⋅( y² + 2y + 4) = 0

(y – 2).1 + (y – 2)⋅( y² + 2y + 4) = 0

• Colocando (y – 2) em evidência:

(y – 2)⋅[1 + ( y² + 2y + 4)] = 0

(y – 2)⋅[1 +  y² + 2y + 4] = 0

(y – 2)⋅( y² + 2y + 5) = 0

∴ y – 2 = 0  ⇾  y = 2

ou

y² + 2y + 5 = 0

• Usando a fórmula de Bhaskara:

• Como 2^x = y  e  y = 2:

2^x = 2   ⇾   2^x = 2¹  ∴ x = 1

• Como 2^x = y:

e 

• Aplicado o logaritmo aos dois membros da equação:

• Aplicando a propriedade:

• Dividindo por log 2 a equação:

• Aplicando a propriedade:

• Solução: