O logaritmo é a operação inversa da exponenciação. Em outras palavras, se

O logaritmo é denotado por loga (x), onde:
“a” é a base do logaritmo.
“x” é o número que está sendo o logaritmado.






Tipos de logaritmos
- Logaritmo natural (ln): base "e" (aproximadamente 2,718)
- Logaritmo comum (log): base 10
- Logaritmo binário (log2): base 2
a) Física: logaritmos são usados para descrever a intensidade de fenômenos como som e luz
b) Engenharia: logaritmos são usados para calcular a magnitude de grandezas como tensão e corrente elétrica
c) Finanças: logaritmos são usados para calcular a taxa de retorno de investimentos
Exercícios

Resolução:


Resposta:
2 - Qual é o valor de x na equação logarítmica?

Resolução:


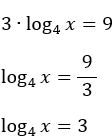

3 - Determine o valor de:
Resolução:





Resolução:

• Usando a definição:




Resposta:









• Usando a propriedade:






Aplicado o logaritmo aos dois membros da equação:
log 62x = log 54


Dividindo ambos os membros da equação por 2:
8 – Resolva a
equação 2x + 23x = 10.
Resolução:
2x +
23x = 10
2x +
(2x)3 = 10
• Fazendo 2x = y:
y + y3
= 10
y + y3
– (2 + 8) = 0
y + y3
– 2 – 8 = 0
y – 2 + y3
– 8 = 0
y – 2 + y3
– 2⋅2⋅2 = 0
y – 2 + y3 – 23= 0
(y – 2) + (y3 – 23) = 0
• Usando a propriedade de fatoração:
a3 – b3 = (a – b)⋅( a2 + ab + b2)
y3 – 23 = (y – 2)⋅( y2 + y⋅2 + 22)
= (y – 2)⋅( y2 + 2y + 4)
• Substituindo em:
(y – 2) + (y3
– 23) = 0
(y – 2) + (y – 2)⋅( y2 + 2y + 4) = 0
(y – 2)⋅1 + (y
– 2)⋅( y2 + 2y + 4) = 0
• Colocando (y –
2) em evidência:
(y – 2)⋅[1 + (
y2 + 2y + 4)] = 0
(y – 2)⋅[1
+ y2 + 2y + 4] = 0
(y – 2)⋅( y2
+ 2y + 5) = 0
y – 2 = 0 ⇒ y = 2
ou
y2 +
2y + 5 = 0
• Usando a fórmula de
Bhaskara:
a = 1, b = 2 e c = 5



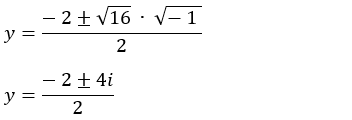
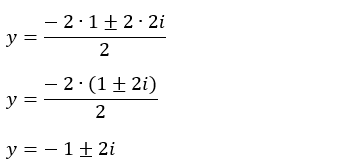
• Como 2x = y e y = 2:
2x = y
• Como 2x = y:

• Aplicado o logaritmo aos dois membros da equação:
• Aplicando a
propriedade:

• Dividindo por log 2 a
equação:

• Aplicando a propriedade:
• Solução:

9 - Qual é o valor de x na equação 4x – 2 = 40?
Resolução:
4x – 2 = 40

• Aplicado o logaritmo
aos dois membros da equação:
• Aplicando a propriedade:

• Dividindo por log 4 a
equação:

• Aplicando a
propriedade:

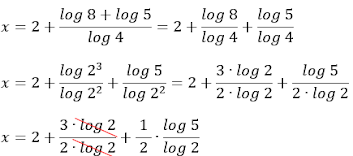
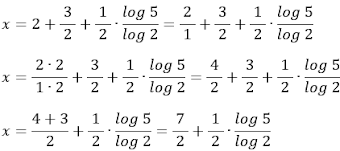
• Aplicando a propriedade:
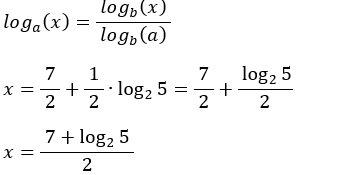
10 – Determine o valor de x na equação 6x ⋅ 6x = 54.
Resolução:
6x ⋅ 6x = 54 ⇒ 6x+x = 54 ⇒ 62x = 54
Aplicado o logaritmo aos dois membros da equação:
log 62x = log
54
Aplicando a propriedade:
Loga (xk) = k⋅ loga (x)
2x⋅log
6
=
log 6⋅9
plicando a propriedade:
loga
(x⋅y) =
loga (x) + loga (y)
2x⋅log
6
=
log 6 + log
9
Dividindo
por log 6 a equação:


Dividindo por log 2 a equação:



