Números binários

Os números binários são a base dos sistemas digitais modernos e da computação. Eles utilizam apenas dois dígitos: 0 e 1. Ao contrário do sistema decimal que usamos no dia a dia (base 10), o sistema binário é baseado em potências de 2.

Conceitos Básicos

1. Dígitos Binários:
• O sistema binário utiliza apenas dois dígitos: 0 e 1. Cada dígito binário é chamado de bit.
2. Posições e Potências de 2:
• 
  Assim como no sistema decimal cada posição representa uma potência de 10, no sistema binário cada posição representa uma potência de 2. Por exemplo, o número binário 1011 pode ser interpretado como:                         

Conversão de Binário para Decimal

Para converter um número binário para decimal, multiplicamos cada dígito binário pela potência de 2 correspondente e somamos os resultados. Vamos converter o número binário 1011 para decimal:

Portanto, 1011 em binário é igual a 11 em decimal.

Exemplos: 

a) 101 (binário) = 1 × 2² + 0 × 2¹ + 1 × 2⁰ 

                          = 1 × 4 + 0 × 2 + 1 × 1

                          = 4 + 0 + 1 = 5 (decimal)

b) 1111 (binário) = 1 × 2³ + 1 × 2² + 1 × 2¹ + 1 × 2⁰

                            = 1 × 8 + 1 × 4 + 1 × 2 + 1 × 1

                            = 8 + 4 + 2 + 1= 15 (decimal)

Representação de números binários

1. Números inteiros: 101 (5 em decimal), 1101 (13 em decimal).

2. Números fracionários: 0,101 (0,625 em decimal).

3. Números negativos: Representados com complemento de dois.

Conversão de números decimais em binário

Fazemos divisões sucessivas por 2.

Exemplos: Converter o número 25 em binário.

Resposta:

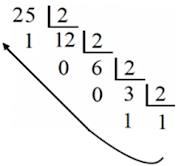
25 (decimal) = 11001 (binário)

Importância na Computação

Os números binários são fundamentais para a operação de computadores e dispositivos digitais porque:

• Circuitos Digitais: Os circuitos eletrônicos operam em dois estados (ligado/desligado), o que se alinha perfeitamente com os dígitos 0 e 1 do sistema binário.

• Processamento de Dados: Computadores processam e armazenam dados em forma binária, utilizando bits e bytes.

Exemplos Práticos

• Armazenamento: Em um byte, que é composto por 8 bits, é possível representar 256 valores diferentes 2⁸.

• Codificação de Dados: Texto, imagens e sons podem ser codificados em binário para armazenamento e processamento digital.

Exercícios

1 - (ENEM) O resultado da adição 9 + 12 será representado, na base binária, por

a) 101

b) 1101

c) 1111.

d) 10101.

e) 11001.

Resolução:

9 + 12 = 21

De modo prático, fazendo as divisões sucessivas:

Resposta:

21 (decimal) = 10101 (binário)

2 – Escreva o número 19 na base 2.

Resolução:

Resposta:

19 (decimal) = 10011 (binário)

3 - Escreva o número 87 na forma de seu equivalente binário.

Resolução:

De modo prático, fazendo as divisões sucessivas por 2:

Resposta:

87 (decimal) = 1010111 (binário)

4 - Converta o número binário 1100101 para base decimal.

1 × 2⁶ + 1 × 2⁵ + 0 × 2⁴ + 0 × 2³ + 1 × 2² + 0 × 2¹ + 1 × 2⁰

= 1 × 64 + 1 × 32 + 0 × 16 + 0 × 8 + 1 × 4 + 0 × 2 + 1 × 1

= 64 + 32 + 0 + 0 + 4 + 0 + 1

= 101

Resposta: 

1100101 (binário) = 101 (decimal)

5 – Converta o número 552 em binário.

Resolução:

Fazendo as divisões sucessivas por 2:

Resposta:

552 (decimal) = 1000101000 (binário)

6 - Determine o valor decimal de cada número sinalizado a seguir na forma complemento de 2:

a) 10010011 (binário)

b) 01011110 (binário)

c) 10110001 (binário)

d) 11001000 (binário)

e) 10101111 (binário)

f) 00110010 (binário)

g) 00100010 (binário)

h) 10001110 (binário)

Resolução:

a) 1 × 2⁷ + 0 × 2⁶ + 0 × 2⁵ + 1 × 2⁴ + 0 × 2³ + 0 × 2² + 1 × 2¹ + 1 × 2⁰

= 1 × 128 + 0 × 64 + 0 × 32 + 1 × 16 + 0 × 8 + 0 × 4 + 1 × 2 + 1 × 1

= 128 + 0 + 0 + 16 + 0 + 0 + 2 + 1

= 147

 b) 0 × 2⁷ + 1 × 2⁶ + 0 × 2⁵ + 1 × 2⁴ + 1 × 2³ + 1 × 2² + 1 × 2¹ + 0 × 2⁰

= 0 × 128 + 1 × 64 + 0 × 32 + 1 × 16 + 1 × 8 + 1 × 4 + 1 × 2 + 0 × 1

= 0 + 64 + 0 + 16 + 8 + 4 + 2 + 0

= 94

 c) 1 × 2⁷ + 0 × 2⁶ + 1 × 2⁵ + 1 × 2⁴ + 0 × 2³ + 0 × 2² + 0 × 2¹ + 1 × 2⁰

= 1 × 128 + 0 × 64 + 1 × 32 + 1 × 16 + 0 × 8 + 0 × 4 + 0 × 2 + 0 × 1

= 128 + 0 + 32 + 16 + 0 + 0 + 0 + 1

= 177

 d) 1 × 2⁷ + 1 × 2⁶ + 0 × 2⁵ + 0 × 2⁴ + 1 × 2³ + 0 × 2² + 0 × 2¹ + 0 × 2⁰

= 1 × 128 + 1 × 64 + 0 × 32 + 0 × 16 + 1 × 8 + 0 × 4 + 0 × 2 + 0 × 1

= 128 + 64 + 0 + 0 + 8 + 0 + 0 + 0

= 200

 e) 1 × 2⁷ + 0 × 2⁶ + 1 × 2⁵ + 0 × 2⁴ + 1 × 2³ + 1 × 2² + 1 × 2¹ + 1 × 2⁰

= 1 × 128 + 0 × 64 + 1 × 32 + 0 × 16 + 1 × 8 + 1 × 4 + 1 × 2 + 1 × 1

= 128 + 0 + 32 + 0 + 8 + 4 + 2 + 1

= 175

 f) 0 × 2⁷ + 0 × 2⁶ + 1 × 2⁵ + 1 × 2⁴ + 0 × 2³ + 0 × 2² + 1 × 2¹ + 0 × 2⁰

= 0 × 128 + 0 × 64 + 1 × 32 + 1 × 16 + 0 × 8 + 0 × 4 + 1 × 2 + 0 × 1

= 0 + 0 + 32 + 16 + 0 + 0 + 2 + 0

= 50

 g) 0 × 2⁷ + 0 × 2⁶ + 1 × 2⁵ + 0 × 2⁴ + 0 × 2³ + 0 × 2² + 1 × 2¹ + 0 × 2⁰

= 0 × 128 + 0 × 64 + 1 × 32 + 0 × 16 + 0 × 8 + 0 × 4 + 1 × 2 + 0 × 1

= 0 + 0 + 32 + 0 + 0 + 0 + 2 + 0

= 34

 h) 1 × 2⁷ + 0 × 2⁶ + 0 × 2⁵ + 0 × 2⁴ + 1 × 2³ + 1 × 2² + 1 × 2¹ + 0 × 2⁰

= 1 × 128 + 0 × 64 + 0 × 32 + 0 × 16 + 1 × 8 + 1 × 4 + 1 × 2 + 0 × 1

= 128 + 0 + 0 + 0 + 8 + 4 + 2 + 0

=142