Equações diferenciais homogêneas de 2ª ordem

São um tipo fundamental de equação diferencial que aparece frequentemente em várias áreas da ciência e da engenharia. Vamos descompactar o que isso significa de forma simples.

Definição
Uma equação diferencial homogênea de segunda ordem é uma equação da forma:

ou

Onde a, b e c são constantes, e y é a função que queremos encontrar.

Características

1. Homogênea: Significa que a equação é igual a zero (não há termos independentes ou forças externas).
2. Segunda Ordem: O termo de maior derivada é a segunda derivada de y.

Solução Geral

A solução geral de uma equação diferencial homogênea de segunda ordem depende das raízes da equação característica associada, que é obtida substituindo

na equação diferencial, resultando na equação quadrática:

Os tipos de soluções dependem da natureza das raízes (r₁ e r₂) dessa equação característica:

1 - Raízes Distintas e Reais (r₁ e r₂): Quando a equação característica tem duas raízes reais e distintas, a solução geral é:    

2 - Raízes Iguais (r₁ = r₂): Quando a equação característica tem uma raiz real dupla, a solução geral é:

    

       

3 - Raízes Complexas Conjugadas (r₁ = α + βi e r₂ = α − βi): Quando a equação característica tem raízes complexas, a solução geral é:

     

Exemplo Prático
Considere a equação diferencial:

ou

Equação característica associada:

Exercícios 
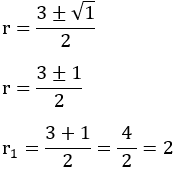
1 - Resolva a equação diferencial:

Resolução:
Equação característica associada:

 

 

 

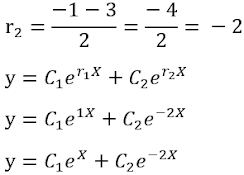
2 - Determine a solução da equação diferencial:

Resolução:

Equação característica associada:

 

 

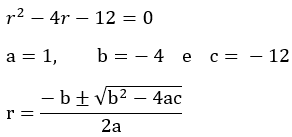
3 - Qual a solução da equação diferencial abaixo?

Resolução:

Equação característica associada:

4 - Resolva as seguintes equações diferenciais:

Resolução:

Equação característica associada:

     

Resolução:

Equação característica associada: