As derivadas parciais são um conceito fundamental no cálculo multivariado, utilizado para analisar funções que dependem de várias variáveis independentes. Elas representam a taxa de variação de uma função em relação a uma de suas variáveis, mantendo as outras constantes.
Definição:

Interpretação:
A derivada parcial ∂f/∂x representa
a taxa de variação da função f em relação à variável x, mantendo as outras
variáveis constantes. Em outras palavras, é a taxa de variação da função ao
longo da direção x.
Exemplos:
f(x, y) = x2y + 3xy2



Notação
Derivadas parciais são usadas em diversas áreas, como:
- Otimização: Encontrar máximos e mínimos de funções de várias variáveis.
- Equações diferenciais parciais: Modelar fenômenos físicos, como a propagação de calor ou ondas.
- Economia: Analisar funções de produção e utilidade.
Resolução:

2 - Encontrar
as derivadas parciais de primeira ordem da função de duas variáveis f(x, y)
= 2xy2.
Resolução:

3 - Dada a função f(x, y) = 2x + 5y2, obtenha:



c)

4 - Considere a função f(x, y) = 5x2 +y4 – 2xy3, obtenha:
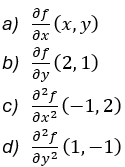








Nenhum comentário:
Postar um comentário