Mudança de base de logaritmo

A mudança de base de logaritmo é uma técnica importante na álgebra e na análise matemática, usada para converter logaritmos de uma base para outra. Esta técnica é útil porque permite simplificar cálculos e resolver equações logarítmicas que envolvem diferentes bases.

                            Conceitos Básicos

Um logaritmo de um número x na base b é definido como o expoente ao qual a base deve ser elevada para obter x:

se e somente se b ^y = x

Fórmula de Mudança de Base

A fórmula de mudança de base para logaritmos é:

Onde:

  é o logaritmo de “a” na base b.

  é o logaritmo de “a” na base c.

   é o logaritmo de “b” na base c.

A base "c" pode ser qualquer base válida, como 10 (logaritmo comum) ou "e" (logaritmo natural).

                          Exemplo de Mudança de Base

Suponha que queremos calcular log₂(8) usando a fórmula de mudança de base com a base 10:

• Usando uma calculadora:

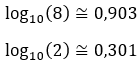
• Portanto:

                          Exercícios

1 - Calcule o valor do logaritmo log₁₀₀​ (72), considerando os valores: 

 e 

Resolução:

log₁₀₀​ (72)

• Vamos transformar a base 100 em base 10 usando a fórmula de mudança de base:

• Fatorando o número 72:

• Usando a propriedade dos produtos:

• Teremos:

• Usando a propriedade da potência:

• Vamos ter:

• Como:

2- Encontre o logaritmo log₃​ (6).

Resolução:

• O argumento é 6 e a base é 3. Podemos usar a fórmula para mudança de bases e escrever como um quociente de logaritmos naturais:

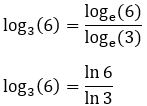
• Usando uma calculadora:

• Arredondarmos para três casas decimais:

3 - (ESPCEX – 2011) Considere log 2 = 0,30 e log 3 = 0,48, o número real x, solução da equação 5^{x – 1} = 150, pertence ao intervalo:

a) ] – ∞, 0[   b) [4, 5]    c) ]1, 3[     d)[ 0, 2[  e) [3, + ∞ [ 

Resolução:

• Usando a definição de logaritmo:

• Fatorando o número 750:

• Usando a propriedade dos produtos:

Fazendo a mudança de base:

• Logo:

4 < x < 5

• Resposta: Letra (b)

4 - Resolva a equação:

Resolução:

• Calculando o logaritmo nos dois membros da equação:

• Usando a propriedade:

• Usando a propriedade:

• Usando a propriedade:

• Usando a propriedade:

5 - Resolva a equação:

Resolução:

• Calculando o logaritmo nos dois membros da equação:

• Usando a propriedade:

• Calculando novamente o logaritmo nos dois membros da equação:

• Usando a propriedade:

• Dividindo ambos os membros da equação por:

• Fazendo novamente a mudança de base:

6 - Resolva a equação exponencial 4^x = 24.

Resolução:

4^x = 24

• Calculando o logaritmo nos dois membros da equação:

• Usando a propriedade:

• Dividindo os dois membros da equação por log 4:

• Fatorando o número 24:

• Usando a propriedade do produto:

• Usando a propriedade:

ou

7 – Considerando log 2 = 0,3, log 3 = 0,48 e log 5 = 0,7, calcule o valor do log₃₆ (0,5).

Resolução:

• Usando a expressão de mudança de base:

• Usando as propriedades:

• Usando a propriedade:

• Logo:

8 –  Resolva a equação 2^x + 2^3x  = 10.

2^x + 2^3x  = 10

2^x + (2^x)³  = 10

• Fazendo 2^x = y:

y + y³ = 10

y + y³ – (2 + 8) = 0

y + y³ – 2 – 8 = 0

y – 2 + y³ – 8 = 0

y – 2 + y³ – 2⋅2⋅2 = 0

(y – 2) + (y³ – 2³) = 0

y³ – 2³ = (y – 2)⋅•( y² + y2 + 2²)

             = (y – 2)⋅( y² + 2y + 4)

• Substituindo em:

(y – 2) + (y³ – 2³) = 0

(y – 2) + (y – 2)⋅( y² + 2y + 4) = 0

(y – 2).1 + (y – 2)⋅( y² + 2y + 4) = 0

• Colocando (y – 2) em evidência:

(y – 2)⋅[1 + ( y² + 2y + 4)] = 0

(y – 2)⋅[1 +  y² + 2y + 4] = 0

(y – 2)⋅( y² + 2y + 5) = 0

∴ y – 2 = 0  ⇾  y = 2

ou

y² + 2y + 5 = 0

• Usando a fórmula de Bhaskara:

• Como 2^x = y  e  y = 2:

2^x = 2   ⇾   2^x = 2¹  ∴ x = 1

• Como 2^x = y:

e 

• Aplicado o logaritmo aos dois membros da equação:

• Aplicando a propriedade:

• Dividindo por log 2 a equação:

• Aplicando a propriedade:

• Solução:

9 - Qual é o valor de x na equação 4^{x – 2} = 40?

Resolução:

• Aplicado o logaritmo aos dois membros da equação:

• Aplicando a propriedade:

• Dividindo por log 4 a equação:

• Aplicando a propriedade:

• Aplicando a propriedade:

10 – Determine o valor de x na equação 6^x ⋅ 6^x = 54.

Resolução:

6^x ⋅ 6^x = 54   ⇒   6^x+x = 54   ⇒   6^2x = 54

Aplicado o logaritmo aos dois membros da equação:

log 6^2x = log 54

Aplicando a propriedade:

Log_a (x^k) = k⋅ log_a (x)

2x⋅log 6 = log 6⋅9

plicando a propriedade:

log_a (x⋅y) = log_a (x) + log_a (y)

2x⋅log 6 = log 6 + log 9

Dividindo por log 6 a equação:

Aplicando a propriedade:

Dividindo por log 2 a equação: