Equações diferenciais ordinárias

Uma equação diferencial é uma equação que envolve uma função desconhecida e suas derivadas. Elas são usadas para modelar fenômenos onde há uma taxa de variação, como o crescimento populacional, a propagação de calor, ou o movimento de um objeto.
Tipos de Equações Diferenciais

1. Equações Diferenciais Ordinárias: Envolvem derivadas em relação a uma única variável independente. Por exemplo:


onde ( y ) é a função desconhecida de ( t ), e ( k ) é uma constante.

2. Equações Diferenciais Parciais: Envolvem derivadas parciais em relação a mais de uma variável independente. Por exemplo:

onde ( u ) é a função desconhecida de ( t ) e ( x ), e ( D ) é uma constante.

Soluções de Equações Diferenciais

As soluções de equações diferenciais podem ser:

Explícitas: A solução é dada diretamente em termos das variáveis independentes.

Implícitas: A solução é dada de forma indireta, onde a função desconhecida não está isolada.

1 - Determine o valor de y na equação diferencial y’ = x².

Resolução:

Calculando a integral em ambos os membros:

2 - Verifique se as funções y = e^2x e y = x³ são soluções da equação diferencial y' – y = e^2x.

Resolução:

Lembrando que:

Substituindo:

em

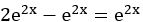
Então:

 (Verdadeira)

Logo, y = e^2x é solução da equação diferencial y' – y = e^2x.

Para:

(Falsa)

Logo, y = x³ não é  solução da equação diferencial y' – y = e^2x.

3 - Verifique se as funções dadas abaixo, são soluções da equação diferencial y' – 3y = 0.

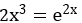
 e  

Resolução:

Substituindo em y' – 3y = 0:

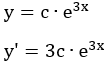
 (Verdadeira)

Para:

y = c ⋅ cos(c)

y' = c ⋅ [– sen(x)]

y' = – sen(x)

Substituindo em y' – 3y = 0:

y' – 3y = 0

– c ⋅ sen(x) – 3⋅ c ⋅ cos(x) = 0 (Falsa)

4 - Verifique se a função y = 1 é solução da equação diferencial y’’+ 2y' + y = x.

Resolução:

y = 1

y’ = 0

y'' = 0

Substituindo esses valores em y'' + 2y' + y = x:

y'' + 2y' + y = x

0 + 0 + 1 = x

1 = x (Falsa)

5 - Verifique se a função dada abaixo é solução da equação diferencial y'' + 2y' + y = 0.

y = 2e^{– x} + xe^{– x}

 Resolução:

Lembrando que (f ⋅ g)’=f’⋅ g + f ⋅ g’:

y’ = 2e^{– x}. (– 1) + 1⋅ e^{– x} + x ⋅ e^{– x}. (– 1)

y’ = – 2e^{– x} + 1e^{– x} – xe^{– x}

y’ = – e^{– x} – xe^{– x}

 y’’ = – e^{– x}. (– 1) – [1⋅ e^{– x} + x ⋅ e^{– x}. (– 1)]

y’’ = e^{– x} – e^{– x} + xe^{– x}

y’’ = xe^{– x}

Substituindo esses valores em y''+ 2y' + y = 0:

y’’+ 2y' + y = 0

xe^{– x} + 2 ⋅ (– e^{– x} – xe^{– x}) + 2e^{– x} + xe^{– x} = 0

xe^{– x} – 2e^{– x} – 2xe^{– x} + 2e^{– x} + xe^{– x} = 0

xe^{– x} + xe^{– x} – 2e^{– x} – 2xe^{– x} + 2e^{– x} = 0

xe^{– x} + xe^{– x} – 2xe^{– x} = 0

2xe^{– x} – 2xe^{– x} = 0

0 = 0 (Verdadeira)

Desvio médio

O desvio médio é uma medida de dispersão que indica o quanto, em média, os valores de um conjunto de dados diferem da média desse conjunto. É uma maneira simples de entender a variabilidade dos dados.

Como calcular o desvio médio:

1. Calcule a média (média aritmética) do conjunto de dados.

2. Subtraia a média de cada valor individual no conjunto para encontrar os desvios individuais.

3. Tome o valor absoluto de cada desvio (isso elimina qualquer diferença negativa).

4. Calcule a média desses valores absolutos.

A fórmula para o desvio médio é:

      

     Onde:

•    x_i são os valores individuais do conjunto de dados.

•  é a média dos valores do conjunto de dados.

• $\mathrm{ \; n}$ é o número total de valores no conjunto.

Vamos ilustrar com um exemplo simples. Suponha que você tenha os seguintes dados: $2, 4, 6, 8, 10$

1º) Calcule a média:

2º) Encontre os desvios individuais e seus valores absolutos:

3º) Calcule a média desses desvios absolutos:

Portanto, o desvio médio do conjunto de dados é 2.4.

Exercícios

1 - Qual é o desvio médio dos pontos 1, 3, 5 e 7? 

Resolução:

Cálculo da média:

Desvios individuais e seus valores absolutos:

Cálculo da média desses desvios absolutos:

2 - Qual o desvio médio da série (3, 4, 5, 6, 7)?

Resolução:

Cálculo da média:

Desvios individuais e seus valores absolutos:

Cálculo da média desses desvios absolutos:

3 – Qual é o desvio médio dos números 2, 10, 12, 3 e 3?

      a) 4          b)   4,4           c)   4,5            d)   5,2            e)   6

 Resolução:

 Cálculo da média:

 

 

 Desvios individuais e seus valores absolutos:

 

 Cálculo da média desses desvios absolutos:

4 - Considere as notas 2, 8, 5 e 6 obtidas por 4 alunos, numa prova de Matemática. Determine o desvio médio das notas.

Resolução:

Cálculo da média das notas: 

Desvios individuais e seus valores absolutos:

Cálculo da média desses desvios absolutos:

5 - Considere os dados do conjunto A = {− 2, − 5, 0, 3, 4}. Qual é o desvio médio desses números?

Resolução:

Cálculo da média desses números: 

Desvios individuais e seus valores absolutos:

Cálculo da média desses desvios absolutos: