A multiplicação de número por todos os seus antecessores até chegar ao número 1, é chamado de Fatorial.
2⋅1
3⋅2⋅1
4⋅3⋅2⋅1
5⋅4⋅3⋅2⋅1
6⋅5⋅4⋅3⋅2⋅1
7⋅6⋅5⋅4⋅3⋅2⋅1
8⋅7⋅6⋅5⋅4⋅3⋅2⋅1
9⋅8⋅7⋅6⋅5⋅4⋅3⋅2⋅1
10⋅9⋅8⋅7⋅6⋅5⋅4⋅3⋅2⋅1

O Fatorial de um número natural inteiro positivo é representado por n!
n! = n⋅(n − 1)⋅(n − 2)⋅ ... ⋅3⋅2⋅1
A notação n! foi introduzida pelo matemático francês Christian Kramp em 1808, nascido em Estrasburgo, Reino da França, em 13 de maio de 1826.
2! = 2⋅1 = 2
3! = 3⋅2⋅1 = 6
4! = 4⋅3⋅2⋅1 = 24
5! = 5⋅4⋅3⋅2⋅1 = 120
6! = 6⋅5⋅4⋅3⋅2⋅1 = 720
7! = 7⋅6⋅5⋅4⋅3⋅2⋅1 = 5040
8! = 8⋅7⋅6⋅5⋅4⋅3⋅2⋅1 = 40320
9! = 9⋅8⋅7⋅6⋅5⋅4⋅3⋅2⋅1 = 362880
10! = 10⋅9⋅8⋅7⋅6⋅5⋅4⋅3⋅2⋅1 = 3628800

Por definição, temos:
0! = 1
1! = 1
Exercícios
1 − Resolva a expressão − 2² + 4!
a) 0 b) 28 c) − 20 d) 20
Resolução:
− 2² + 4! = − 2⋅2 + 4⋅3⋅2⋅1
= − 4 + 12⋅2
= − 4 + 24
= 20
2 − Simplifique as frações:

Resolução:



3 − (FEI-SP) Se (n + 4)! + (n + 3)! = 15(n + 2)!, então:
a) n = 4 b) n = 3 c) n = 2 d) n = 1 e) n = 0
Resolução:
(n + 4)⋅(n + 3)⋅(n + 2)! + (n + 3)⋅(n + 2)! = 15(n + 2)!
(n + 4)⋅(n + 3) + (n + 3) = 15
n⋅n + n⋅3 + 4⋅n + 4⋅3 + n + 3= 15
n² + 3n + 4n + 12 + n + 3 = 15
n² + 8n + 15 − 15 = 0
n² + 8n = 0
n⋅(n + 8) = 0
n = 0
ou
n + 8 = 0 ⇒ n = − 8 (não convém)
Solução: n = 0
4 − Quanto é 80 - 100:2?
a) 0 b) 1 c) 3 d) 5! e) 5#
Resolução:
80 – 100:2 = 80 – 50 = 30
5! = 5⋅4⋅3⋅2⋅1 = 120
5# = 5⋅3⋅2 = 30
Resposta: Letra E
5 − Qual é o valor da expressão 30 – 10:2 – 1?
a) 24! b) 4! c) 8! d) 9
Resolução:
30 – 10:2 – 1
= 30 – 5 – 1
= 25 – 1 = 24
Como 4! = 4⋅3⋅2⋅1 = 24
Resposta Letra B
6 − O valor de
é:
a) 1 b) 52 c) 2 916 d) 53 921
Resolução:
Colocando 53! em evidência:
7 − Simplifique a expressão:
Resolução:
8 − Simplifique a expressão abaixo:
Resolução:
9 − (PUC-RS) Se
então n é igual a:
a) n = 13 b) n = 11 c) n = 9 d) n = 8 e) n = 6
Resolução:
Colocando (n −1)! em evidência no denominador:
n = − 9 (não convém)
Solução: n = 9
10 - (Unitau-SP) Sendo n ≠ 0, o(s) valor(es) de n, tal que
é (são):
a) 7. b) 0 e 7. c) 0 e 10. d) 1. e) 0 e 2.
Resolução:
Colocando (n – 1)! em evidência:
Colocando “n” em evidência:
ou
n – 7 = 0 ⇒ n = 7
Resposta: Letra A.
11 − Resolva a seguinte equação:
a) n = 5 b) n = 6 c) n = 7 d) n = 8 e) n = 9
Resolução:
n = − 7 (não convém)
Solução: n = 8
12 − Encontre o valor de "n" na equação (n!)2 – 25n! + 24 = 0.
Resolução:
(n!)² – 25n! + 24 = 0.
Fazendo n! = x
x2 – 25x + 24 = 0
Como n! = x
n! = 24 = 4⋅3⋅2 = 4⋅3⋅2⋅1 = 4!
n! = 4! ⇒ n = 4
n! = 1 = 1!
n! = 1! ⇒ n = 1
Solução: n = 1 ou n = 4
13 − Se
então:
a) n = 2 b) n = 12 c) n = 5 d) n = 7 e) n = 10
Resolução:
Colocando n! em evidência no denominador:
n = − 9 (Não convém)
Solução: n = 5
14 – Resolva e equação:
Resolução:

Usando a fórmula resolutiva:
n2 negativo não
convém.
Solução: n = 2
15 − Resolva a equação fatorial:
• Vamos fazer x2 + 9x + 19 = t
• Para t = – 41
x2 + 9x + 19 = t
x2 + 9x + 19 = – 41
x2 + 9x + 19 + 41 = 0
x2 + 9x + 60 = 0
• Usando a fórmula de Bhaskara:

Solução não realPara t = 41:
x2 + 9x + 19 = t
x2 + 9x + 19 = 41
x2 + 9x + 19 – 41 = 0
x2 + 9x – 22 = 0
• Usando a fórmula de Bhaskara para a equação:
Fatorial negativo não serve!
• Para x = 2
• Solução: x = 2
16 − Resolva a equação fatorial:
Resolução:
Colocando (n + 1)n! em evidência:
Multiplicando cruzado:
(n + 1)(n + 3) = 48
n2 + 3n + n + 3 = 48
n2 + 4n + 3 – 48 = 0
n2 + 4n – 45 = 0
Usando a fórmula resolutiva:
a =1, b = 4
e c = –
45
Como n2 é negativo, não convém.
Solução: n = 5







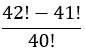









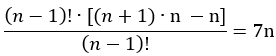








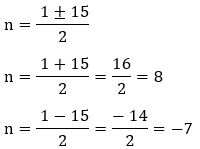



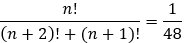


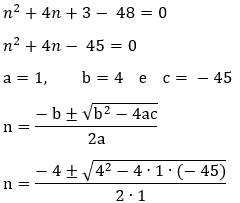






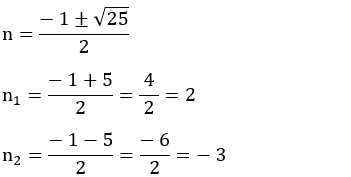


















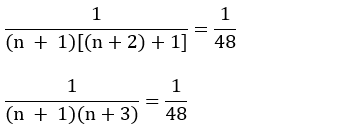
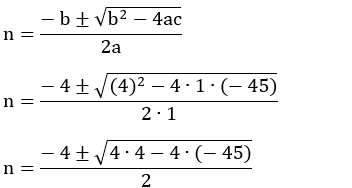




Nenhum comentário:
Postar um comentário