Razões trigonométricas

As razões (ou relações) trigonométricas estão relacionadas com os ângulos de um triângulo retângulo. As principais são: o seno, o cosseno e a tangente. As relações trigonométricas são resultado da divisão entre as medidas de dois lados de um triângulo retângulo, e por isso são chamadas de razões.As razões (ou relações) trigonométricas estão relacionadas com os ângulos de um triângulo retângulo. As principais são: o seno, o cosseno e a tangente. As relações trigonométricas são resultado da divisão entre as medidas de dois lados de um triângulo retângulo, e por isso são chamadas de razões.Você

A trigonometria é a parte da matemática que lida com o estudo dos triângulos, especialmente os triângulos retângulos, e as relações entre seus ângulos e lados. Ela é fundamental em várias áreas, como engenharia, física, astronomia e até mesmo na música.

As razões (ou relações) trigonométricas estão relacionadas com os ângulos de um triângulo retângulo. As principais são: o seno, o cosseno e a tangente. As relações trigonométricas são resultado da divisão entre as medidas de dois lados de um triângulo retângulo, e por isso são chamadas de razões.

Razões trigonométricas no triângulo retângulo

Seno (sen): Em um triângulo retângulo, o seno de um ângulo é a razão entre o comprimento do cateto oposto ao ângulo e o comprimento da hipotenusa.

Cosseno (cos): O cosseno de um ângulo é a razão entre o comprimento do cateto adjacente ao ângulo e o comprimento da hipotenusa. 

Tangente (tg): A tangente de um ângulo é a razão entre o comprimento do cateto oposto ao ângulo e o comprimento do cateto adjacente. 

Identidades Trigonométricas

Existem várias identidades trigonométricas importantes que são usadas para simplificar expressões e resolver equações. Algumas das mais comuns são:

• Identidade de Pitágoras:

• Identidade da Tangente:

Ângulos Comuns

As tabelas trigonométricas geralmente incluem valores para ângulos comuns, como 0°, 30°, 45°, 60° e 90°. Aqui estão alguns exemplos dos valores dessas funções:

Ө	0º	30º	45º	60º	90º
Seno (Ө)	0				1
Cosseno (Ө)	1				0
tangente (Ө)	0		1		Indefinido

Exemplos

1 – Qual é o valor de y?

Resolução:

• Na tabela:

2 – Na figura a seguir, há um triângulo retângulo com um de seus ângulos agudos medindo 60°. Determine o comprimento do lado representado pela letra x, em centímetros.

Resolução:

• Na tabela:

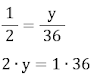
3 –  Encontre a medida x no triângulo retângulo:

Resolução:

4 – (CEDERJ 2021) Estudando para uma prova de trigonometria, Júlia aprendeu que sen² 72° é igual a

Resolução:

• Vamos usar a identidade de Pitágoras:

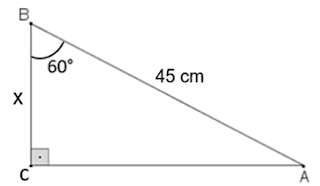
5 – Determine os valores de x e y no triângulo retângulo da figura:

Resolução:

ou como:

ou como:

6 – Num triângulo retângulo o cosseno de um ângulo B é igual a 1/3. Qual é o seno desse mesmo ângulo?

Resolução:

• Vamos usar a identidade de Pitágoras:

7 – De acordo com os dados a figura, qual é a altura x do prédio?

Resolução:

• Comparando (1) e (2):

• Colocando x em evidência:

• Racionalizando o denominador da fração:

• Lembrando que:

• Fazendo:

8 – Na figura abaixo, a árvore é vista sob um ângulo de 30°, a uma distância de 30 metros de sua base. A altura da árvore, em metros, é:

Use 

Resolução:

• Cateto oposto: x

• Cateto adjacente: 30 m

9 - Qual é o valor de x no triângulo retângulo da figura?

Resolução:

10 - (Unifor-CE) Na figura abaixo tem-se um observador em O, que vê o topo de um prédio sob o ângulo de 45°. A partir desse ponto, afastando-se do prédio 8 m, ele atinge o ponto A, de onde passa a ver o topo do mesmo prédio sob um ângulo θ tal que tg θ = 6/7.

A altura do prédio, em metros é:

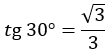
Resolução:

• Fazendo a altura do prédio igual a x:

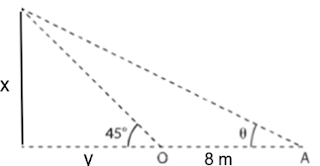
• Como tg 45° = 1, vamos ter:

ou

v = x          (2)

• Substituindo (2) em (1):

  x = 48 m

11 - (IFPE) Após a instalação de um poste de energia, há a orientação de que ele fique apoiado por um período de 48 horas, após a sua fixação no terreno, por meio de 4 cabos de sustentação. A figura a seguir ilustra um modelo de um desses cabos de sustentação. Sabendo que o cabo de sustentação do poste forma um ângulo de 60° com a vertical e que ele está conectado ao poste a uma altura de 10 metros, determine o comprimento mínimo do cabo. 

a) 10 𝑚

b) 5 𝑚

c) 25 𝑚

d) 20 𝑚

e) 12 𝑚

Resolução:

• Chamando de x a medida do comprimento do cabo:

• Como:

• Multiplicando cruzado:

• Resposta: Letra (d)