A regra de três é usada na proporção, para medir a relação entre grandezas que são diretamente proporcionais, ou seja, que o aumento de uma implica no aumento da outra, ou ainda que são inversamente proporcionais, quando o aumento de uma implica na redução da outra.
A regra de três simples também é muito utilizada em situações que envolvam cálculos financeiros, misturas químicas, conversões de grandezas na Física.
Na regra de três simples, conhecemos três valores e desconhecemos apenas um. Multiplicamos cruzado e chegamos ao resultado. É preciso, no entanto, analisar se são diretamente proporcionais ou inversamente proporcionais. Veja os passos:
- Crie uma tabela e agrupe as grandezas da mesma espécie na mesma coluna.
- Identificar se as grandezas são inversamente ou diretamente proporcionais, analisaremos isso no próximo passo.
- Montar a equação assim: se as grandezas forem diretamente proporcionais, multiplicamos os valores em cruz, isto é, em forma de X. Se as grandezas forem inversamente proporcionais, invertemos os valores para ficarem diretamente proporcional.
- Resolva a equação.
Exercícios
1 – Quanto é 60% de R$ 500,00?
Resolução:
% Reais

Grandezas diretamente proporcionais:

x = 300 reais.
2 – Um quilo de farinha de trigo é suficiente para fazer 12 pães. De quanta farinha necessito para fazer 18 pães?
Resolução:
kg Pães

Grandezas diretamente proporcionais:

x = 1,5 kg
3 – Os R$ 200,00 que Lucas tem correspondem a 40% do valor que ele tinha. Qual era o valor principal?
Resolução:
% Reais

Grandezas diretamente proporcionais:

X = 500
4 – Para se construir uma parede de 25 m² são necessários 2 pedreiros. Quantos pedreiros serão necessários para construir uma parede de 150 m²?
Resolução:
m² Pedreiros

Grandezas diretamente proporcionais:
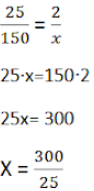
x = 12
Resposta: 12 pedreiros.
Resolução:
R$ Dias

Grandezas diretamente proporcionais:


Resposta: Esta pessoa terá que trabalhar 20 dias.
6 – Para se construir um muro de 17 m² são necessários 3 trabalhadores. Quantos trabalhadores serão necessários para construir um muro de 51 m² ?
Resolução:
m² Trabalhadores
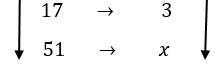
Grandezas diretamente proporcionais:

x = 9
Resposta: 9 trabalhadores
7 – Com uma área de absorção de raios solares de 1,2 m², uma lancha com motor movido a energia solar consegue produzir 400 watts por hora de energia. Aumentando-se essa área para 1,5 m², qual será a energia produzida?
Resolução:
m² watts

Grandezas diretamente proporcionais:

x = 500
Resposta: A energia produzida será de 500 watts.
8 – Um automóvel consome, em média, 8 litros de álcool num trecho de 72 km . O consumo desse automóvel em 126 km será de:
a) 12 litros
b) 14 litros
c) 16 litros
d) 18 litros
Resolução:
Resolução:
Litros km

Grandezas diretamente proporcionais:

72 ∙ x = 8 ∙ 126
72 ∙ x = 8 ∙ 126
72x = 1008

x = 14 litros
9 – Um torneira despeja 15 litros de água por minuto. Para encher um tanque de 1800 litros , ela leva:
a) 1 hora
b) 2 horas
c) 90 minutos
d) 150 minutos
Resolução:
Litros Minutos

10 – Se 15 operários levam 10 dias para completar um certo trabalho, quantos operários farão esse mesmo trabalho em 6 dias?
Resolução:
Resolução:
Operários Dias

6∙x = 15∙10
6x = 150
x = 25
Resposta: 25 operários.
12 – Em 5 horas, uma
máquina produz 120 peças. Quantas peças ela produzirá em 8 horas?
Resolução:
Horas Peças

Grandezas diretamente proporcionais:

X = 192 peças
Nenhum comentário:
Postar um comentário