Ângulos suplementares

Ângulos suplementares são um conceito importante na geometria. Dois ângulos são chamados de suplementares quando a soma de suas medidas é igual a 180 graus. Em outras palavras, se você tem dois ângulos “a” e “b”, eles são suplementares se:

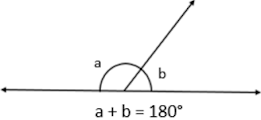
Aqui estão alguns pontos chave sobre ângulos suplementares:

1. Linha Reta: Ângulos suplementares frequentemente aparecem quando dois ângulos compartilham um lado em comum e juntos formam uma linha reta. Por exemplo, se um ângulo é 120 graus, o ângulo suplementar a ele será 180°−120° = 60°.
2. Geometria de Polígonos: Ângulos suplementares também são relevantes em polígonos. Por exemplo, os ângulos internos de um quadrado formam pares de ângulos suplementares.
3. Aplicações Práticas: Entender ângulos suplementares é útil em diversas áreas, como arquitetura, engenharia e até arte, onde a medida precisa e a construção de ângulos são cruciais.

Vamos ver um exemplo prático: Suponha que você tenha um ângulo de 75 graus. O ângulo suplementar a ele seria 180° − 75° = 105°.

Exercícios

1 – Dois ângulos são suplementares. Se um deles tem medida de 20º, qual a medida do outro? 

Resolução:

x + 20º = 180º

x = 180º – 20º

x = 160º

2 – Vamos calcular o valor de x nas figuras abaixo:

a) 

Resolução:

3x + 10º + 50º = 180º

3x + 60º = 180º

3x = 180º –  60º

3x = 120º

x = 40º

b) 

Resolução:

x + 90º + 2x = 180º

x + 2x = 180º – 90º

x + 2x = 180º – 90º

3x = 90º

x = 90º/3

x = 30º

       

c) 

Resolução:
2x + 20º + 2x = 180º

2x + 2x = 180º – 20º

4x = 160º

x = 40º

3 –  Determine o valor de x e as medidas de cada um dos ângulos abaixo.

Resolução:

3x – 10º + 2x – 40° = 180° 

5x – 50º = 180° 

5x  = 180° + 50º

5x  = 230º

x = 46º

3x – 10º = 3 ⋅ 46° – 10º = 138° – 10° = 128°

2x – 40° = 2 ⋅ 46° – 40° = 92° – 40° = 52°

Resposta: x = 46° e os ângulos medem 128° e 52°.