Exercícios com equações biquadradas

Equação biquadrada é toda equação do 4º grau que pode ser reduzida em equação quadrática.

Equação biquadrada:

ax⁴ + bx²  + c = 0

Fazendo: x⁴  = (x²)².

a(x²)² + bx² + c = 0

Transformando: x² = y

Equação quadrática

Exercícios:

1 - Resolver a equação biquadrada x⁴ – 5x²  + 4 = 0, sendo U = IR:

Resolução:

Transformando em equação do 2º grau:

x⁴ – 5x²  + 4 = 0

Fazendo: x² = y

Como x² = y

Solução:

x = 1, x = – 1, x = 2 e x = – 2

2 - Resolver a equação biquadrada x⁴ + 2x²  – 3 = 0, sendo U = IR:

Resolução:

Transformando em equação do 2º grau:

x⁴ +  2x²  – 3 = 0

Fazendo: x² = y

Solução: x = 1 e x = – 1

3 - Resolver a equação biquadrada x⁴ + 4x²  – 12 = 0, sendo U = IR.

Resolução:

Transformando em equação do 2º grau:

x⁴ + 4x²  – 12 = 0

Fazendo: x² = y

Solução:

4 - Resolver a equação biquadrada x⁴ = x² + 1, sendo U = IR.

Resolução:

Fazendo x² = y:

Vamos usar a fórmula de Bhaskara para resolver essa equação do 2º grau: 

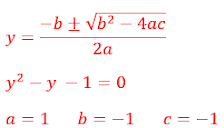
Como 1–< 0:

Solução:

ou

5 - Resolva a equação biquadrada x⁴ – 100x² + 2304 = 0.

Resolução:

Transformando essa em equação do 2º grau:

Fazendo:

Como:

Resposta: x = 6, x = – 6, x = 8 ou x = – 8.