Dizemos que uma função é crescente quando ela apresenta maiores valores para y = f(x), quando também aumentamos os valores de x. Enquanto isso, classificamos uma função como decrescente quando, para maiores valores de x, obtemos menores valores para y = f(x).
a > 0: função crescente;
a < 0: função decrescente.
Para melhor compreender essas definições, veja alguns exemplos. Observe:
Função crescente
Um exemplo de função crescente é a função y = 2x – 1.
Para perceber isso, observe a tabela a seguir:
x | y |
0 | – 1 |
1 | 1 |
2 | 3 |
3 | 5 |
4 | 7 |
Observe que o valor de x, a cada linha, é aumentado em uma unidade. Consequentemente, realizando-se os cálculos de y a partir da função dada, percebemos que, a cada linha, o valor dessa variável aumenta em quatro unidades.
Função decrescente
Uma função decrescente é aquela em que o valor da variável y diminui sempre que a variável x aumenta. Um exemplo de função decrescente é a seguinte: y = – 2x + 9. Para perceber isso, observe a tabela a seguir:
x | y |
0 | 9 |
1 | 7 |
2 | 5 |
3 | 3 |
4 | 1 |
Observe que, cada vez que o valor de x aumenta uma unidade, o valor de y diminui três unidades. Dessa maneira, essa função é decrescente.
Exercícios
1 - Indique se a função abaixo é crescente ou decrescente:
A função cuja lei de formação é y = – 3x + 4.
b) Decrescente
2 - Indique se a função abaixo é crescente ou decrescente:
A função cuja lei de formação é y = 2x + 5.
a) Crescente
b) Decrescente
3 - A função representada no gráfico abaixo é crescente ou decrescente:

A alternativa correta é:
a) Crescente
b) Decrescente
Resposta: Aumentado valores de x, obtemos maiores valores para y = f(x). (Crescente)
4 - A função representada no gráfico abaixo é crescente ou decrescente:

a) Crescente
b) Decrescente
















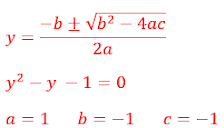


 < 0:
< 0: 


























