É uma equação
que, no primeiro ou no segundo membro, tem termos em módulo. Para resolver
problemas de equação modular, devemos aplicar a definição de módulo.
|x| = x, se x ≥
0
|x| = – x, se x
< 0
Exemplos
1 – Resolva a
equação modular |x – 2| = 7.
Resolução:
• Usando a
definição de módulo:
|x – 2| = 7 ⇒ x – 2 = 7 ⇒ x = 7 + 2 ∴ x = 9
ou
|x – 2| = – 7 ⇒ x – 2 = – 7 ⇒ x – 2 = – 7 + 2 ∴ x = – 5
• Solução: {9, –
5}2 – Qual é a
solução da equação modular |2x – 1| = |– x + 5|?
Resolução:
• Usando a
definição de módulo:|2x – 1| = |– x + 5|
2x – 1 = – x + 5 ⇒ 2x + x = 5 + 1
3x = 6 ∴ x = 2
ou
2x – 1 = – (– x + 5) ⇒ 2x – 1 = x – 5
2x – x = – 5 + 1 ∴ x = – 4
• Solução: {2, – 4}
3 – Determinar
a solução da equação |x2 – 5x| = 6.
Resolução:
• Usando a
definição de módulo:
|x2 – 5x| = 6 ⇒ x2 – 5x = 6 ⇒ x2 – 5x – 6 = 0
ou
|x2 – 5x| = – 6 ⇒ x2 – 5x = – 6 ⇒ x2 – 5x + 6 = 0
• Para x2 – 5x – 6 = 0:
a = 1, b = – 5
e c = – 6


• Para x2 – 5x + 6 = 0:
a = 1, b = – 5
e c = 6


Exercícios
1 – Qual é a
solução da equação modular |2x – 1| = – 3?
Resolução:
|2x – 1| = – 3
• Pela definição de módulo:
S = ∅
2 – Determinar
a solução da equação||x – 3| – 1|= 6.
Resolução:
||x – 3| – 1|= 6
|x – 3| – 1 = 6 ou |x
– 3| – 1 = – 6
|x – 3| = 6 + 1 |x – 3| = – 6 + 1
|x – 3| = 7 |x – 3| = – 5 (Não existe!)
x – 3 = 7
x = 7 + 3
x = 10
ou
x – 3 = – 7
x = – 7 + 3
x = – 4
Solução: {10, –
4}
3 – Resolva a
equação |x|2 – 3|x| = 0.
Resolução:
|x|2 – 3|x| = 0
S = ∅
2 – Determinar
a solução da equação||x – 3| – 1|= 6.
Resolução:
||x – 3| – 1|= 6
|x – 3| – 1 = 6 ou |x
– 3| – 1 = – 6
|x – 3| = 6 + 1 |x – 3| = – 6 + 1
|x – 3| = 7 |x – 3| = – 5 (Não existe!)
x – 3 = 7
x = 7 + 3
x = 10
ou
x – 3 = – 7
x = – 7 + 3
x = – 4
Solução: {10, –
4}
3 – Resolva a
equação |x|2 – 3|x| = 0.
Resolução:
|x|2 – 3|x| = 0
• Fazendo |x|= y:
y2 –
3y = 0
y2 –
3y = 0
• Colocando y em evidência:
y(y – 3) = 0
y = 0
ou
y – 3 = 0 ⇒ y = 3
y(y – 3) = 0
y = 0
ou
y – 3 = 0 ⇒ y = 3
• Substituindo o valor de y em |x|= y:
|x|= 0 x = 0
e
|x|= 3 x = 3 ou x = – 3
|x|= 0 x = 0
e
|x|= 3 x = 3 ou x = – 3
• Solução: {– 3, 0, 3}
4 - Sabendo que as
soluções da equação |x|2 – |x| – 6 = 0 são raízes da equação x2
– ax + b = 0, podemos afirmar que:
c) a = 1 e b = – 6.
d) a = 0 e b = – 9.
e) não existe a e b tais que x2 – ax + b = 0 contenha as raízes da equação dada.
Resolução:
|x|2
– |x| – 6 = 0
• Fazendo |x| = y:
y2 – y – 6 = 0
• Usando a fórmula de Bhaskara:
a = 1, b = – 1 e c
= – 6
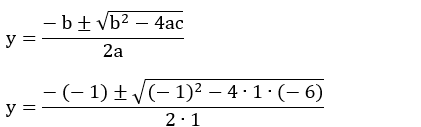

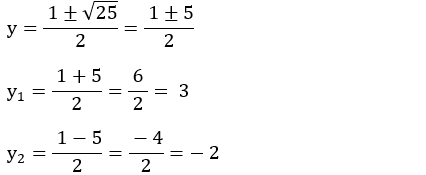
• Como |x| = y:
e
|x| = – 2 Não existe!
• Substituindo x
= 3 e x = – 3 em:
x2 – ax + b = 0
32 – a⋅3 + b = 0 ⇒ – 3a + b = – 9 (1)
e
(– 3)2 – a⋅ (– 3) + b = 0 ⇒ 3a + b = – 9 (2)
• Somando (1) com (2):
3a + b = – 9
• Substituindo o
valor de b em (2):
3a = 0 ⇒ a = 0
• Resposta: Letra D
Nenhum comentário:
Postar um comentário