Inequação exponencial

Uma inequação exponencial é uma desigualdade que envolve uma variável no expoente. Essas inequações são importantes em várias áreas da matemática e são frequentemente encontradas em problemas de crescimento e decaimento exponencial, bem como em aplicações práticas como a modelagem de populações, finanças e física.

Passos básicos para resolver inequações exponenciais:

1. Identifique a inequação exponencial: Normalmente, ela terá a forma a^x > b, a^x < b, a^x ≥ b ou a^x ≤ b, onde a e b são constantes, e x é a variável.
2. Isolar o termo exponencial: Tente deixar a expressão na forma a^x sozinha em um dos lados da inequação.
3. Utilize logaritmos: Para resolver a inequação, você pode aplicar logaritmos dos dois lados da inequação. Isso permitirá que você "traga o expoente para baixo" e trabalhe com uma inequação linear ou polinomial.

Exemplo: 

Para a inequação 2^x > 5, você pode aplicar logaritmos (usando base 2 ou logaritmo natural):

      log (2^x) > log (5)

      Usando propriedades de logaritmos:

      x⋅log (2) > log (5)

     

      Fazendo uma mudança de base: 

      

Considere a base do expoente: Se a base a é maior que 1, a função exponencial é crescente, então a direção da desigualdade permanece a mesma ao tomar logaritmos. Se a base aa está entre 0 e 1, a função exponencial é decrescente, então a direção da desigualdade se inverte ao tomar logaritmos.

4. Resolva a inequação resultante: Depois de aplicar os logaritmos, resolva a inequação para a variável x.

Exemplo prático:

 Vamos resolver a inequação 3^2x ≤ 9.

1. Primeiro, reconhecemos que 9 pode ser escrito como 3²:

          3^2x ≤ 3²

2. Como as bases são iguais, podemos comparar os expoentes:

          2x ≤ 2

3. Dividindo ambos os lados por 2:

          x ≤ 1

          Portanto, a solução para a inequação é x ≤ 1.

Resumindo:

Para 

Para  

Exercícios 

1 – Qual é a solução da inequação exponencial:

Resolução:

S = {x ∈ ℝ| x > 2}

2 – Resolva a inequação exponencial 2^x ≥ 128.

Resolução:

2^x ≥ 128

Fatorando o número 128:

2^x ≥ 2⁷  ∴   x ≥ 7

S = {x ∈ ℝ| x ≥ 7}

3 – Resolva as inequações exponenciais em ℝ:

Resolução:

a) 2^{x + 7} < 32

Fatorando o número 32:

2^{x + 7} <  2⁵   ∴   x + 7 < 5

x < 5 – 7    ⇒    x < – 2

S = {x ∈ ℝ| x < – 2}

(2^{- 1})^{x + 1} ≥ (2²)^{x + 3}

2 ^{- x - 1} ≥ 2^{2x + 6}   ∴  – x – 1 ≥ 2x + 6

– x – 2x ≥ 6 + 1 ⇒  – 3x ≥ 7    X(– 1)

Solução:

4 – Resolva a inequação exponencial:

Resolução:

∴  – 6x + 15 ≤ – 3x – 3

– 6x + 3x ≤ – 3 – 15

– 3x ≤ – 18    X(– 1)

3x ≥ 18

S = {x ∈ ℝ| x ≥ 6}

5 – Resolva a inequação exponencial:

Resolução:

Solução:

6 – O conjunto solução da inequação

é:

a)( – ∞; 5]

b) [5; + ∞)

c) [– 5; + ∞)

d) [4; + ∞)

e) (– ∞; – 5]

Resolução:

Solução:

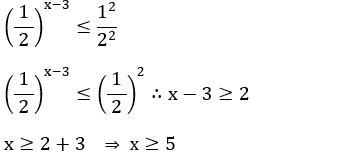
S = {x ∈ ℝ| x ≥ 5} ou  S = [5; + ∞)
 

Inequações modulares

Uma inequação modular é uma expressão matemática que envolve módulos (ou valores absolutos). A função módulo, denotada por |x|, representa a distância de x até zero na reta numérica, sempre resultando em um valor não negativo. 

Por exemplo, |3| = 3 e ∣−3∣ = 3.

Definições de inequações modulares

|x| > a ⇒ x > a ou x < – a

|x| < a ⇒ x < a ou x > – a

|x| ≥ a ⇒ x ≥ a ou x ≤ – a

|x| ≤ a ⇒ x ≤ a ou x ≥ – a   

Exemplos de inequações modulares

1. Simples:
• |x| < 3 significa que os valores de x estão a menos de 3 unidades de distância de 0. Isso se traduz na inequação − 3 < x < 3.
2. Mais complexas:
• |x − 2| > 5 significa que a distância entre x e 2 é maior que 5. Isso se traduz em duas inequações: x −2 > 5 ou x − 2 < − 5, resultando em x > 7 ou x < − 3.

Passos para resolver inequações modulares

1. Entender a definição do módulo:
• Transforme a inequação modular em duas inequações sem módulo, conforme a definição de valor absoluto.
2. Resolver cada uma das inequações resultantes:
• Trabalhe com cada uma das desigualdades separadamente e encontre as soluções.
3. Unir as soluções:
• Combine os intervalos de solução obtidos para determinar o intervalo total de solução.

Exemplo 1

Resolver ∣x +1∣ ≤ 4.

1. Remover o módulo:
• − 4 ≤ x + 1 ≤ 4.
2. Isolar x:
• Subtrair 1 de todos os lados: 
• − 5 ≤ x ≤ 3.

A solução é o intervalo x ∈ [− 5; 3].

Exemplo 2

Resolver ∣2x −3∣ > 7.

1. Remover o módulo:
• 2x – 3 > 7 ou 2x – 3 < − 7.
2. Resolver cada desigualdade:
• 2x > 10 ou 2x < − 4.
• x > 5 ou x < − 2.

Solução: x ∈ (−∞, −2) ∪ (5, ∞).

Exercícios

1 – Resolva a equação modular |x – 1| < 4.

x – 1 < 4     ou      x – 1 > – 4.

x < 4 + 1               x > – 4 + 1

x < 5                        x > – 3

S = ] – 3; 5[ 

2 – Resolva a equação modular |2x – 1| ≥ x + 1.

Resolução:

|2x – 1| ≥ x + 1

2x – 1 ≥ x + 1    ou    2x – 1 ≤ – (x + 1)

2x – 1 ≥ x + 1            2x – 1 ≤ – (x + 1)

2x – x ≥ 1 + 1            2x – 1 ≤ – x – 1

x ≥ 2                          2x + x ≤ – 1 + 1

                                  3x ≤ 0

                                  x ≤ 0

       S = {𝑥 ∈ ℝ | x ≤ 0 ou x ≥ 2}

       ou

       S = ] − ∞, 0 ] Ս [2, + ∞[

3 – Dada a equação modular |x² – 5x + 2| < 2, qual é sua solução?

Resolução:

|x² – 5x + 2| < 2

x² – 5x + 2 < 2       ou    x² – 5x + 2 > – 2

x² – 5x + 2 – 2 < 0         x² – 5x + 2 + 2 > 0

x² – 5x < 0                     x² – 5x + 4 > 0

x = 0 ou x = 5                x = 1 ou x = 4

  

            

S = ]0; 1[  Ս  ]4; 5[

4 – Resolva a equação modular |2x – 1| > |x + 3|.

Resolução:

|2x – 1| > |x + 3|

2x – 1 > x + 3       ou     2x – 1 < – (x + 3)

2x – x > 3 + 1                2x – 1 < – x – 3

x > 4                               2x + x < – 3 + 1

                                       3x < – 2 

  

          S = ] –∞; – 2/3 [ Ս ] 4; +∞[

5 – Resolva as seguintes inequações modulares:

a) |x + 3| < 4

b) 2|3 – x| ≥ 5

Resolução:

a) |x + 3| < 4

x + 3 < 4           e           x + 3 > – 4

x < 4 – 3                   x > – 4 – 3

x < 1                        x > – 7

S = ] – 7; 1[

b) 2|3 – x| ≥ 5

2(3 – x) ≥ 5      ou     2(3 – x) ≤ – 5   

6 – 2x ≥ 5                  6 – 2x ≤ – 5

– 2x ≥ 5 – 6               – 2x ≤ – 5 – 6

– 2x ≥ – 1 ⋅ (– 1)      – 2x ≤ – 11 ⋅ (– 1)      

2x ≤ 1                        2x ≥ 11

Solução: x ∈ ] −∞, ½] ∪ [11/2, ∞[

6 – Quais números inteiros satisfazem a desigualdade 1 ≤ |– 2x + 3|  ≤ 4.

Vamos dividir essa inequação em duas partes:  

Primeira parte: |– 2x + 3| ≥ 1     

– 2x + 3 ≥ 1         ou         – 2x + 3 ≤ – 1

– 2x ≥ 1 – 3                      – 2x ≤ – 1 – 3

– 2x ≥ – 2   ⋅ (– 1)            – 2x ≤ – 4  ⋅ (– 1)

2x ≤ 2                               2x ≥ 4

Segunda parte: |– 2x + 3| ≤ 4

– 2x + 3 ≤ 4        ou      – 2x + 3 ≥ – 4

– 2x ≤ 4 – 3                  – 2x ≥ – 4 – 3

– 2x ≤ 1 ⋅ (– 1)             – 2x ≥ – 7 ⋅ (– 1)

2x ≤ – 1                        2x ≥ 7 

   

Resposta: Os números inteiros que satisfazem a desigualdade são: 0, 1, 2, e  3.

Equação da circunferência

A equação geral da circunferência é x² + y² – 2ax – 2by + a² + b² – r² = 0. Já a equação reduzida da circunferência no plano cartesiano é (𝑥 − 𝑎)² + (𝑦 − 𝑏)² = 𝑟². 

Equação geral da circunferência

• A equação geral da circunferência pode ser obtida a partir da equação reduzida. 
• Para obter a equação geral, basta desenvolver os produtos notáveis da equação reduzida

Equação reduzida da circunferência 

• A equação reduzida da circunferência é utilizada para representar a circunferência no plano cartesiano.
• Para encontrar a equação reduzida de uma circunferência, é preciso conhecer o raio e as coordenadas do centro.

(𝑥 − 𝑎)² + (𝑦 − 𝑏)² = 𝑟²

Na equação, C(a, b) representa as coordenadas do centro da circunferência e 𝑟 é o comprimento do raio.

          

Exemplos

• a equação (x − 3 + (y − 4)² = 169  ⇒  (x − 3)² + (y − 4)² = 13², representa uma circunferência com centro em C(3,4) e raio r =13.

• a equação x² + y² = 0  ⇒   (x – 0)² + (y – 0)² = 0², representa uma circunferência centrada na origem O(0, 0)do sistema de coordenadas e raio 0.

• a equação (x + 4)² + (y – 4)² = 81  ⇒  (x + 4)² + (y – 4)² = 9², representa uma circunferência de centro C (– 4, 4) e raio 9.

• a equação x² + (y – 3)² = 25   ⇒   (x – 0)² + (y – 3)² = 5², representa uma circunferência de centro C(0 ,3) e raio 5.

Comprimento da circunferência

• O comprimento da circunferência é calculado pela fórmula C = 2πr. 
• O comprimento da circunferência é igual a duas vezes o raio vezes o número pi. 

Área do círculo delimitado por uma circunferência

• Para calcular a área da círculo, multiplique o quadrado do valor do raio por π.
• A = πr²

Transição da equação geral da circunferência para a equação reduzida:

Exemplo: Um a circunferência possui centro em C(4, 2) e raio 5. Sabendo dessas informações, determine a equação geral dessa circunferência.

• Fazendo a = 4,   b = 2   e   r = 5 em:

x² + y² – 2ax – 2by + a² + b² – r² = 0

x² + y² – 2⋅4⋅x – 2⋅2⋅y + 4² + 2² – 5² = 0

x² + y² – 8x – 4y + 16 + 4 – 25 = 0

x² + y² – 8x – 4y + 20 – 25 = 0

x² + y² – 8x – 4y – 5 = 0

Exercícios

1 - A equação geral da circunferência que possui raio 6 e centro C(3, – 4) é? 

a) x² + y² + 6x – 5 = 6

b) (x – 3)² + (y + 4)² = 36

c) (x + 3)² + (y – 4)² = 36

d) x² + y² – 6x + 8y – 11 = 0

e) x² + y² + 6x + 8y + 11 = 0

Resolução: 

• Fazendo a = 3,   b = – 4   e   r = 6 em:

x² + y² – 2ax – 2by + a² + b² – r² = 0

x² + y² – 2⋅3⋅x – 2⋅ (– 4) ⋅y + 3² + (– 4)² – 6² = 0

x² + y² – 6x + 8y + 9 + (+ 16) – 36 = 0

x² + y² – 6x + 8y + 9 + 16 – 36 = 0

x² + y² – 6x + 8y – 11 = 0

2 - Escreva a equação reduzida da circunferência de centro C(6, 3) e raio 4.

Resolução:  

• Fazendo a = 6,   b = 3   e   r = 4 em:

(𝑥 − 𝑎)² + (𝑦 − 𝑏)² = 𝑟²

(𝑥 − 6)² + (𝑦 − 3)² = 4²

(𝑥 − 6)² + (𝑦 − 3)² = 16

3 - Dada a equação geral da circunferência x² + y² – 12x + 4y – 9 = 0, determine.

a) o centro C e a medida do raio r dessa circunferência;

b) o comprimento dessa circunferência;

c) a área do círculo delimitado por essa circunferência.

Resolução:  

a) x² + y² – 12x + 4y – 9 = 0

• Somando 6² e 2² em ambos os membros da equação:

x² + y² – 12x + 6² + 4y + 2² = 9 + 6² + 2²

x² + y² – 12x + 6² + 4y + 2² = 9 + 36 + 4

x²– 2⋅6⋅x + 6² + y² + 2⋅2⋅y + 2² = 49

• Usando a fatoração de trinômio quadrado perfeito:

a² + 2ab + b² = (a + b)²

a² – 2ab + b² = (a – b)²

(x – 6)² + (y + 2)² = 7²

• Comparando com a expressão:

(x – a)² + (y – b)² = r² 

• Teremos: Centro C(6, – 2) e o raio r = 7.

b) Fazendo r = 7  e   π = 3,14 em:

C = 2πr
C = 6,28⋅7

C = 43,96 unidades de comprimento

c) A = πr²
A = 3,14⋅7²
A = 3,14⋅49
A = 153,86 unidades de área

Reta numérica real

 A reta numérica real é uma representação visual de todos os números reais em uma linha contínua. Imagine uma linha infinita que se estende em ambas as direções, com um ponto específico marcado como zero (0). À direita do zero, temos os números positivos (1, 2, 3, ...) e à esquerda do zero, temos os números negativos (– 1, – 2, – 3, ...). Cada ponto na reta numérica corresponde a um número real único.

Propriedades Importantes da Reta Numérica Real:

1. Densidade: Entre quaisquer dois números reais distintos, sempre existe outro número real. Por exemplo, entre 1 e 2, podemos encontrar 1,5. Entre 1 e 1,5, podemos encontrar 1,25, e assim por diante.
2. Ordenação: A reta numérica está ordenada. Isto significa que, se tivermos dois números reais a e b tal que a < b, então aa está à esquerda de b na reta numérica.
3. Continuidade: A reta numérica é contínua, sem lacunas. Cada ponto na reta representa um número real, incluindo números irracionais como π e .

Utilidades da Reta Numérica:

• Representação de Operações Aritméticas: A adição e a subtração podem ser visualizadas como movimentos para a direita ou para a esquerda na reta. Por exemplo, adicionar 3 a 2 é como mover 3 unidades à direita de 2.
• Análise de Funções: As funções matemáticas podem ser representadas graficamente na reta numérica, ajudando na visualização de suas propriedades.
• Resolução de Desigualdades: Podemos usar a reta numérica para representar soluções de desigualdades. Por exemplo, a solução de x > 1 é representada como todos os pontos à direita do 1.

 Exemplos

1 - Observe abaixo a reta numérica, dividida em segmentos de mesma medida.

          

O ponto P, está melhor representado pelo número

a) 3,10     b) 3,20     c) 3,25     d) 3,50     e) 3,75

2 - Observe abaixo os cincos pontos marcados na reta real, dividida em segmentos de mesma medida.

          

O número real – 1,87 está melhor representado nessa reta pelo ponto

a) K           b) L.           c) M.           d) N.           e) P. 

3 - (Vunesp) Considere a seguinte reta numerada, na qual estão marcados apenas alguns números:

O número representado pela fração – 3/2, se fosse colocado nessa reta, ficaria entre:
A) 0 e – 1
B) – 1 e – 2
C) – 2 e – 3
D) – 3 e – 4
E) – 4 e – 5

4 - A posição de  a reta numérica está indicada com a seta vermelha. 

          

Qual seria a indicação da posição na reta numérica abaixo?

          

Marque a alternativa correta.

a) A          b) B          c) C          d) D

5 - Represente na reta numerada os números: – 3,4 e .

 

Respostas:

1) 1:4 = 0,25

     3 + 0,25 = 3,25

     Letra C

2)

          

 O número real – 1,87 está entre – 2 e –1: Logo, a resposta é o ponto L.

3) O número – 1,5 está compreendido entre – 1 e – 2.

4) Como , a melhor aproximação é e a letra (D):

5)