Integral

A integral é uma ferramenta matemática que nos permite calcular áreas, volumes e muitas outras grandezas. Imagine que você tem uma curva desenhada em um gráfico. A integral nos ajuda a descobrir a área exata abaixo dessa curva em um determinado intervalo.

Em resumo:
⇾ Área: A integral calcula a área sob uma curva.
⇾ Acumulação: Ela representa a acumulação de uma grandeza ao longo do tempo ou de um intervalo.
⇾ Inversa da derivada: A integração é, em certo sentido, a operação inversa da derivação.

Tipos de integrais:

⇾ Definida: Calcula a área em um intervalo específico.
⇾ Indefinida: Encontra a família de funções cuja derivada é a função original.

Integrais imediatas:

Exemplos:

1– Determine:

Resolução:

2 – Calcule a integral:

Resolução:

Para resolver essa integral, vamos usar o produto notável:

3 – Calcule a integral:

Resolução:

4 – Calcular a área sob a curva da função f(x) = x² no intervalo de 0 a 2.

Resolução:

Resposta: a área é igual a 8/3 unidades de área.

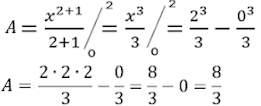
5 – Calcule o valor da integral definida abaixo:

Resolução:

Resposta: O valor da integral 81/4 unidades de área