As equações literais do 2º grau são aquelas que contêm coeficientes literais, ou seja, letras que representam números desconhecidos ou variáveis. Essas equações podem ser expressas da forma geral ax2 + bx + c = 0, onde:
- a,
b e c são coeficientes literais ou constantes;
- x
é a variável ou incógnita que queremos determinar.
Para resolver uma equação literal do 2º grau, podemos
seguir os seguintes passos:
- Verifique
se a equação está na forma padrão: Certifique-se de que a
equação esteja organizada na forma ax2 + bx + c = 0.
- Identifique
os coeficientes: Anote os valores de a, b e c.
- Calcule
o discriminante (Δ): O discriminante é dado por
Δ = b2 – 4ac. Ele nos ajuda a
determinar o número e a natureza das raízes da equação.
- Se
Δ > 0, a equação tem duas raízes reais e distintas.
- Se
Δ = 0, a equação tem uma raiz real dupla (ou duas raízes iguais).
- Se
Δ < 0, a equação tem duas raízes complexas conjugadas.
- Calcule
as raízes: Usando a fórmula de Bhaskara, podemos
encontrar as raízes da equação:

Exemplos
1 - Suponha que temos a equação 3x2 + 5x + k = 0. Queremos encontrar k de tal forma que a equação tenha apenas uma raiz real. Para isso, precisamos que Δ = 0:
a = 3, b = 5 e c = kΔ = b2 − 4ac = 52 − 4⋅3⋅k
Para Δ = 0, temos:
25 −12k = 0
25 = 12k
Portanto, para que a equação tenha uma única raiz real, k
deve ser igual a 12/25.
2 - Resolva a equação literal 5x2 – 80a2 = 0, sendo x a incógnita.
5x2 – 80a2 = 0 ⇒ 5x2 = 80a2
3 – Para que valores de k a equação literal 2x2 + 4x
+ 5k = 0, admita raízes reais e diferentes?
a = 2, b = 4 e
c = 5k
Δ = b2 – 4ac
Δ = 42 – 4⋅2⋅5k
Δ = 4⋅4 – 8⋅5kPara isso, precisamos que Δ > 0:
16 – 40k > 0 ⇒ – 40k > –16
Multiplicando todos os membros dessa desigualdade por (– 1):
40k < 16

Exercícios
1 – Resolva a equação literal 4x2 – 100m2 = 0, sendo x a incógnita.
Resolução:
4x2 – 100m2 = 0

2 – Resolva a equação literal 8x2 – 3ax =
0, sendo x a incógnita.
Resolução:
8x2 – 3ax = 0
Colocando x em evidência:
x⋅(8x – 3a ) = 0
x =
0
ou
8x – 3a = 0 ⇒ 8x = 3a
Resolução:
x2 – 3mx + 2m2 = 0
a = 1, b = – 3m e c =
2m2
Δ = b2 – 4ac
Δ = (– 3m)2 – 4⋅1⋅2m2
Δ = 9m2 – 8m2
Δ = m2

Solução: {2m; m}
4 – Para que valores de k a equação literal x2 – 2x +
k – 2 = 0, admita raízes reais e iguais?
Resolução:
x2 – 2x + k – 2 = 0
a = 1, b = – 2 e
c = k – 2
Δ = b2 – 4ac
Δ = (– 2)2 – 4⋅1⋅(k –
2)
Δ = (– 2)⋅(– 2) – 4⋅(k –
2)
Δ = 4 – 4k +
8
Δ = 12 – 4k
Para isso, precisamos que Δ = 0:
12 – 4k = 0 ⇒ – 4k = – 12
5 – Resolva a equação literal x2 – (a – b)x – ab = 0, na variável x.
Resolução:
x2 – (a – b)x – ab = 0
a = 1, b = – (a – b) e c =
–
ab
Δ = b2 – 4ac
Δ = (– a + b)2 – 4⋅1⋅(– ab)
Δ = a2 – 2ab + b2 + 4ab
Δ = a2 + 2ab + b2
Δ = (a + b)2



Solução: {0; a + b}
6 – Resolva a equação literal x2 – 3ax + 2a2 = 0 (a > 0).
Resolução:
a = 1, b = – 3a e c =
2a2
Δ = b2 – 4ac
Δ = (– 3a)2 – 4⋅1⋅2a2
Δ = 9a2 – 8a2
Δ = a2

Solução: {x1 = 2a e x2
= a}
Solução: {x1
= 2a e
x2 = a}
7 – Para que valores de
k a equação literal 9x2 + 12x + 2m = 0, não admita raízes
reais?
Resolução:
9x2 + 12x +
2m = 0
a = 9, b = 12
e c = 2m
Δ = b2
– 4ac
Δ = 122 – 4⋅9⋅2m
Δ = 12⋅12 – 36⋅2m
Δ = 144 – 72m
Para isso, precisamos que Δ < 0:
144 – 72m < 0 ⇒ – 72m < –144
Multiplicando
todos os membros dessa desigualdade por (– 1):
– 72m < –144 ⋅ (– 1)
8 – Resolva
a equação literal (x –
k)2
+ (x + k)2 = 6k2,
sendo x a incógnita.
(x – k)2 + (x + k)2
= 6k2
x2 – 2kx + k2 + x2 + 2kx + k2 = 6k2
2x2 + 2k2 – 6k2 = 0
2x2 – 4k2 = 0
Dividindo ambos os
membros dessa equação por 2:
2x2:2 – 4k2:2 = 0 ⇒ x2 – 2k2 = 0
x2 = 2k2
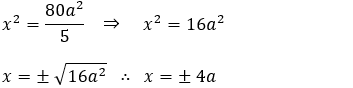

Nenhum comentário:
Postar um comentário