Divisão de polinômios

A divisão de polinômios é um conceito fundamental na álgebra que se assemelha bastante à divisão de números. Ela envolve dividir um polinômio (o dividendo) por outro (o divisor) para obter um quociente e, em alguns casos, um resto.

Imagine que você tem um polinômio P(x) e deseja dividi-lo por um outro polinômio D(x). O objetivo é encontrar dois polinômios: o quociente Q(x) e o resto R(x), de forma que a seguinte igualdade seja válida:

P(x) = Q(x)⋅D(x) + R(x)

Aqui estão algumas características importantes:

• O grau do resto R(x) deve ser menor que o grau do divisor D(x).
• Se o resto for zero, isso significa que D(x) é um divisor exato de P(x).

A divisão de polinômios pode ser feita por diferentes métodos, como o método de chaves, o método de Descartes e o dispositivo prático de Briot-Ruffini.

O dispositivo prático de Briot-Ruffini é uma ferramenta mecânica usada para a realização de operações de divisão de polinômios, em particular, para encontrar o quociente e o resto de uma divisão de polinômios. Desenvolvido pelos matemáticos franceses Briot e Ruffini no século XIX, ele é uma versão prática do método algébrico que hoje é conhecido como o método de divisão sintética.

A principal aplicação desse dispositivo é facilitar a resolução de divisões de polinômios de maneira mais rápida e eficiente, sendo bastante útil no ensino de álgebra. O método permite que se dividam polinômios de forma simplificada, com uma redução do número de operações necessárias, evitando o uso de longas fórmulas e cálculos tradicionais.

Exemplo:

Vamos dividir polinômio P(x) = x³ − 3x² + 5x – 6 pelo divisor D(x) = x − 2.

Passos:

1. Divida o termo de maior grau de P(x) pelo termo de maior grau de D(x):

          

         Este é o primeiro termo do quociente. 

       2. Multiplique x² por D(x) e subtraia o resultado de P(x):

         (x³ − 3x² + 5x − 6) − (x³ − 2x²) = − x² + 5x – 6

      3. Agora, divida o termo de maior grau do novo polinômio pelo termo de maior grau de D(x):
 
          
         Este é o próximo termo do quociente.

 
     4. Multiplique − x por D(x) e subtraia:

         (− x² + 5x − 6) − (− x² + 2x) = 3x − 6

 
     5. Repita o processo:

          

Multiplicando e subtraindo:

(3x − 6) − (3x − 6) = 0

Resultado: O quociente é Q(x) = x² − x + 3 e o resto é R(x) = 0. Isso significa que P(x) é divisível por D(x) sem deixar resto.

Exercícios

1 - Qual é o resto da divisão do polinômio x³ – 6x² + 11x – 6 por x – 2?

Resolução:

Vamos usar o método das chaves:

          

Resposta: O resto da divisão é zero.

2 - (CPACN) Sejam as funções f e g, definidas por f(x) = x⁶ – 2x⁵ – x⁴ + 10x³ – 16x² – 8x + 16 e g(x) = x³ – x² – 4x + 4. A soma dos valores inteiros que satisfazem a desigualdade

é igual a:

a) – 2      b) – 1      c) 0      d) 1      e) 2

Resolução:

• Primeiramente, vamos calcular o quociente, lembrando da condição de existência:

g(x) ≠ 0

 x³ – x² – 4x + 4 ≠ 0

x²⋅(x – 1) – 4⋅(x – 1) ≠ 0

(x – 1)⋅(x² – 4) ≠ 0

x – 1 ≠ 0 ⇒ x ≠ 1

e

x² – 4 ≠ 0   ⇒    x² ≠ 4      

x ≠ 2  e  x ≠ – 2

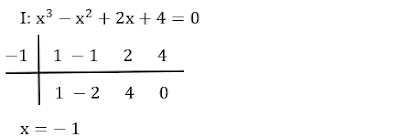
• Usando a fórmula de Bhaskara:

(Não inteiro)

ou

• Usando a fórmula de Bhaskara:

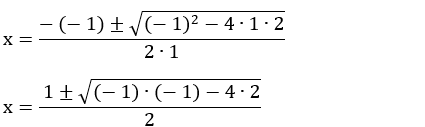
(Não inteiro)

• Soma: S = – 1 + 0 = – 1

• Resposta: Letra B