Função exponencial

Uma função exponencial é uma função matemática da forma f(x) = a⋅b^x, onde:

• a é uma constante diferente de zero,
• b é a base (um número real positivo diferente de 1),
• x é o expoente (a variável independente).

Características Principais:

1. Crescimento Rápido: As funções exponenciais crescem (ou decrescem) muito mais rápido que as funções lineares ou polinomiais.
2. Domínio e Imagem:
• O domínio da função exponencial é todos os números reais ℝ.
• A imagem (ou contradomínio) é o conjunto dos números reais positivos (0, ∞) quando a base b é maior que 1, e (0, ∞) quando 0 < b < 1.
3. Assíntota Horizontal: A reta y = 0 (o eixo x) é uma assíntota horizontal para a função exponencial, indicando que a função se aproxima de zero mas nunca o toca.
4. Passagem pela Origem: Para f(x) = b^x, a função passa pelo ponto (0, 1), porque qualquer número positivo elevado a zero é 1.

Exemplo Prático:

Imagine uma população de bactérias que dobra de quantidade a cada hora. Se começamos com 1 bactéria, após 1 hora teremos 2 bactérias, após 2 horas teremos 4, após 3 horas teremos 8, e assim por diante. Este é um exemplo clássico de crescimento exponencial, que pode ser modelado pela função f(x) = 2^x.  

      

Exercícios

1 - Observe o expoente e verifique quais das sentenças dadas correspondem à lei de uma função exponencial.

Resolução: 

• Apenas a opção (c) não corresponde à lei de uma função exponencial, pois a variável não está no expoente.

2 - Numa certa cultura de bactérias o número delas y cresce segundo a lei y = 20 ⋅ 3^x na qual x representa o tempo em horas. Após quantas horas o número de bactérias será 1620?

Resolução:

y = 20 ⋅ 3^x

• Fazendo y = 1620:

1620 = 20 ⋅ 3^x

81 = 3^x

3⋅3⋅3⋅3 = 3^x

3⁴ = 3^x

x = 4 horas

3 - (CONED – 2016 – Sesc – PA) Qual a soma das raízes ou zeros da função exponencial abaixo?  

f(x) = 2^2x-3 – 3⋅2^x-1 + 4
a) 5          b) 4          c) 6          d) 8          e) – 6

Resolução:

• Para encontrar as raízes ou zeros da função, vamos fazer f(x) = 0:

2^{2x - 3} – 3⋅2^{x -1} + 4 = 0

• Multiplicando por 8 ambos os membros da equação:

• Simplificando a equação:

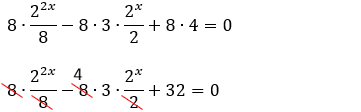
 2^2x – 12⋅2^x + 32 = 0

• Trocando a ordem dos expoentes:

(2^x)² – 12⋅2^x + 32 = 0

Fazendo y = 2^x:

y² – 12y + 32 = 0

• Usando a fórmula de Bhaskara:

a = 1,      b = – 12    e   c = 32

• Como y = 2^x:

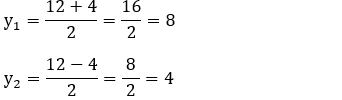
y₁ = 8

8 = 2^x    ⇒   2³ = 2^x    ∴   x = 3

ou

y₂ = 4

4 = 2^x    ⇒   2² = 2^x    ∴   x = 2

• Logo, a soma das raízes é 3 + 2 = 5

• Resposta: Letra A 

4 – Considere a função 

de lei f(x) = 2^x + 1. Determine:

a)) f(1)

b) f(– 3)

c) x quando f(x) = 17

Resolução:

a) f(x) = 2^x + 1

f(1) = 2¹ + 1 = 2 + 1 = 3

b) f(x) = 2^x + 1

f(– 3) = 2^–3 + 1

c) f(x) = 17

 f(x) = 2^x + 1

2^x + 1 = 17     ⇒     2^x = 17 – 1  ⇒    2^x = 16

2^x  =2⋅2⋅2⋅2   ⇒   2^x  = 2⁴   ∴    x = 4

5 – Determinar a lei de formação da função f(x) da figura.

          

Resolução:

• A curva intercepta o eixo y em 2.

• Para x = 1, y = 4.

• Escolhendo dois pontos do gráfico, temos (0,2) e (1,4).

• Em (0,2) temos x = 0 e y = 2:

y = a⋅b^x

2 = a⋅b⁰

2 = a⋅1   ⇒    a = 2

• Em (1, 4) temos x = 1 e y = 4:

y = a⋅b^x

4 = a⋅b¹

4 = a⋅b   ⇒    4 = a⋅2   ⇒   a = 2

• Substituindo a = 2 e b = 2, temos:

f(x) = 2⋅2^x