A regra de três composta é um método pelo qual podemos resolver problemas que envolvem mais de duas grandezas. Esses problemas podem envolver grandezas direta ou inversamente proporcionais e estão presentes em muitas situações do nosso cotidiano.
Usamos as setinhas para facilitar a visualização do aumento ou diminuição dos valores das grandezas: Sempre do número menor para o maior, veja alguns modelos:
1➝ 3 15 ➝ 80 9 ➝ 20
Veja um exemplo:
1 - Em 3 horas, 2 torneiras despejam 2100 litros de água em uma piscina. Então, quantas horas 5 dessas torneiras despejam 7000 litros de água?
Para resolver uma regra de três composta, para facilitar nossa compreensão, montamos uma tabela com as grandezas envolvidas:
Tempo(Horas) Torneiras Volume(Litros)

Inversamente Diretamente
Comparamos a grandeza que tem o x com as demais grandezas: tempo com torneiras e tempo com volume: aumentando o número de torneiras, o tempo irá reduzir (Grandezas inversamente proporcionais) e aumentando o volume, o tempo também aumentará (Grandezas diretamente proporcionais).
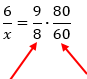
Na montagem das proporções, invertemos os números de torneiras:
Simplificando: Cortando dois zeros no numerador e no denominador:

Multiplicando cruzado:
x⋅105 = 3⋅140
105x = 420
2 - Para fazer uma viagem, rodando uma média de 8 horas por dia a uma velocidade média de 60 km/h, levamos 6 dias para completá-lo. Se dirigir 9 horas por dia à velocidade média de 80km/h, quantos dias, levaremos para completar o percurso dessa viagem?
a) 6 dias
b) 5 dias e meio
c) 4 dias
d) 5 dias
Resolução:
Vamos montar uma tabela com as grandezas envolvidas:
Tempo(Dias) Horas/dia Velocidade(km/h)
Inversamente Inversamente
Comparamos a grandeza que tem o x com as demais grandezas: tempo com horas/dias e tempo com velocidade: aumentando o número de horas/dia, o tempo irá reduzir (Grandezas inversamente proporcionais) e aumentando o velocidade, o tempo irá reduzir (Grandezas inversamente proporcionais).
Na montagem das proporções, invertemos os números de horas/dia e a velocidade:
Invertido Invertido
Simplificando:
Multiplicando cruzado:
x⋅9 = 6⋅69x = 36
x = 4 dias
3 - A quantidade de ração utilizada para alimentar 10 cachorros em um canil, durante 15 dias, é de 60 kg. Caso fossem 18 cachorros no canil, em quantos dias, 36 kg dessa ração duraria?
a) 6 dias
b) 5 dias
c) 4 dias
d) 8 dias
Resolução:
Vamos montar uma tabela com as grandezas envolvidas:
Dias Ração(kg) Cachorros

Diretamente Inversamente
Comparamos a grandeza que tem o x com as demais grandezas: tempo com ração e tempo com cachorros: aumentando o número de cachorros, o tempo irá reduzir (Grandezas inversamente proporcionais) e reduzindo a ração, o tempo irá reduzir (Grandezas diretamente proporcionais).
Na montagem das proporções, invertemos o número de cachorros:
Invertido
Simplificando:
Dividindo 6 por 6 e 36 por 6:Dividindo 6 por 6 e 18 por 6:
Multiplicando cruzado:
x⋅ 3 = 15⋅ 13x = 15
4 - Num canil encontra-se 3 cães farejadores. Sabendo que para alimentá-los durante 9 dias é necessário um pacote de ração de 90 quilogramas, quantos quilogramas de ração serão necessários para alimentar 5 cães por 27 dias?
a) 270
b) 350
c) 400
d) 450
Resolução:
Ração(kg) Cães Dias
Setas vermelhas: Diretamente proporcionais
Setas verdes: Diretamente proporcionais


5 - (Santa Casa - SP) Sabe-se que quatro máquinas, operando 4 horas
por dia, durante 4 dias, produzem 4 toneladas de um certo produto. Quantas
toneladas do mesmo produto seriam produzidas por 6 máquinas daquele tipo,
operando 6 horas por dia, durante 6 dias?
a) 8
b) 15
c) 10,5
d) 13,5
Resolução:
Maquinas Horas/dia Dias Toneladas










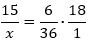












Nenhum comentário:
Postar um comentário