Progressão Geométrica(PG)

 Uma Progressão Geométrica é uma sequência de números onde cada termo, a partir do segundo, é obtido multiplicando o termo anterior por uma constante chamada razão (q). Por exemplo, na sequência 2, 6, 18, 54, ..., a razão é 3.

Características de uma Progressão Geométrica

1. Primeiro Termo (a₁): O primeiro número da sequência.

2. Razão (q): O fator constante pelo qual cada termo é multiplicado para obter o próximo termo.

Fórmula do n-ésimo Termo:

O n-ésimo termo de uma PG pode ser encontrado usando a fórmula:

Onde:

• a_n é o n-ésimo termo.

• a₁ é o primeiro termo.

• q é a razão.

• n é a posição do termo na sequência.

Exemplos

1 - Considere a PG: 2, 6, 18, 54, ... 

Para encontrar o 4º termo:

2 - Obtenha o sexto termo da PG (7, 14, ...).

Resolução:

Cálculo da razão:

Cálculo do sexto termo:

Soma dos termos de uma P. G. finita 

Para encontrar a soma dos termos de uma PG finita, podemos usar a seguinte fórmula:

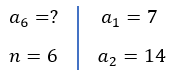
Onde:

• a₁ é o primeiro termo da PG.

• $q$ é a razão da PG.

Exemplo: Calcular a soma dos 5 primeiros termos da P. G. (9, 27, ...).

Resolução:

Soma dos termos de uma PG infinita

Para uma PG infinita, a soma dos termos só é possível se a razão (q) estiver entre -1 e 1 (ou seja, -1 < q < 1). Isso porque, se a razão for maior ou igual a 1 ou menor ou igual a -1, a soma dos termos diverge (vai para infinito).

A fórmula para a soma $S$ de uma PG infinita é:

Onde:

• a₁ é o primeiro termo da PG.

• $q$ é a razão da PG.

Exemplo

Considere a PG infinita: 1, 0.5, 0.25, 0.125, ... 

Aplicando a fórmula: