Problemas com mínimo múltiplo comum

1 - Um relógio A bate a cada 15 minutos, outro relógio B bate a cada 25 minutos, e um terceiro relógio C a cada 40 minutos. Qual é em horas, o menor intervalo de tempo decorrido entre duas batidas simultânea dos três relógios?

Resolução:

Calculando o mínimo múltiplo comum dos números 15, 25 e 40:

Uma hora = 60 minutos

600 : 60 = 10

Resposta: 10 horas 

2 - Três luminosos acendem em intervalos regulares. O primeiro a cada 20 segundos, o segundo, a cada 24 segundos e o terceiro a cada 30 segundos. Se, em um dado instante, os três acenderem ao mesmo tempo, depois de quantos segundos os luminosos voltarão a acender simultaneamente? 

Resolução:

Calculando o mínimo múltiplo comum dos números 20, 24 e 30:

Resposta: Os luminosos voltarão a acender simultaneamente e 120 segundos.

3 - O médico receitou dois tipos de remédio para Mariana. De acordo com as instruções teria de tomar um deles de 8 em 8 horas e o outro de 12 em 12 horas. se ao meio-dia mariana tomou os dois remédios ao mesmo tempo em quantas horas isso ocorrerá novamente?

Resolução:

Calculando o mínimo múltiplo comum dos números 8 e 12:

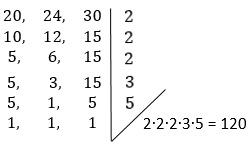
Resposta: 24 horas depois, isto é no dia seguinte ao meio-dia. 

4 - Três pessoas estão jantando juntas em um restaurante. A primeira janta nesse restaurante de 8 3m 8 dias, a segunda, de 15 em 15 dias e a terceira de 10 em 10 dias. Quando ocorrerá o próximo encontro?

Resolução:

Calculando o mínimo múltiplo comum dos números 8, 15 e 10:

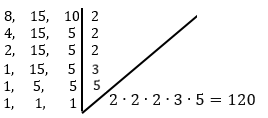
Resposta: O próximo encontro ocorrerá em 120 dias.

5 - Em uma classe existem menos de 40 alunos. Se o professor de Educação Física resolver formar grupos de 6 alunos, ou de 10 alunos, ou de 15 alunos, sempre sobra um aluno. Quantos alunos tem a classe? 

M (6) = {0, 6, 12, 18, 24, (30), 36, ...}

M(10) = {0, 10, 20, (30), 40, 50, 60, ...}

M (15) = {0, 15, (30), 45, 60, 75, ...}

30 + 1 = 31

Resposta: Na classe tem 31 alunos.

Progressão Geométrica(PG)

 Uma Progressão Geométrica é uma sequência de números onde cada termo, a partir do segundo, é obtido multiplicando o termo anterior por uma constante chamada razão (q). Por exemplo, na sequência 2, 6, 18, 54, ..., a razão é 3.

Características de uma Progressão Geométrica

1. Primeiro Termo (a₁): O primeiro número da sequência.

2. Razão (q): O fator constante pelo qual cada termo é multiplicado para obter o próximo termo.

Fórmula do n-ésimo Termo:

O n-ésimo termo de uma PG pode ser encontrado usando a fórmula:

Onde:

• a_n é o n-ésimo termo.

• a₁ é o primeiro termo.

• q é a razão.

• n é a posição do termo na sequência.

Exemplos

1 - Considere a PG: 2, 6, 18, 54, ... 

Para encontrar o 4º termo:

2 - Obtenha o sexto termo da PG (7, 14, ...).

Resolução:

Cálculo da razão:

Cálculo do sexto termo:

Soma dos termos de uma P. G. finita 

Para encontrar a soma dos termos de uma PG finita, podemos usar a seguinte fórmula:

Onde:

• a₁ é o primeiro termo da PG.

• $q$ é a razão da PG.

Exemplo: Calcular a soma dos 5 primeiros termos da P. G. (9, 27, ...).

Resolução:

Soma dos termos de uma PG infinita

Para uma PG infinita, a soma dos termos só é possível se a razão (q) estiver entre -1 e 1 (ou seja, -1 < q < 1). Isso porque, se a razão for maior ou igual a 1 ou menor ou igual a -1, a soma dos termos diverge (vai para infinito).

A fórmula para a soma $S$ de uma PG infinita é:

Onde:

• a₁ é o primeiro termo da PG.

• $q$ é a razão da PG.

Exemplo

Considere a PG infinita: 1, 0.5, 0.25, 0.125, ... 

Aplicando a fórmula:

Sistema de equações do 2º grau

1 - Resolva o sistema de equações do 2° grau:

Resolução:

Isolando y em (2):

y = 3 – x     (3)

Substituindo (3) em (1):

Como y = 3 – x:

Para x = 2

y = 3 – x
y = 3 – 2
y = 1
Para x = 1
y = 3 – x
y = 3 – 1
y = 2

Solução:

x = 2 e y = 1 ou x = 1 e y = 2

2 - Resolva o sistema de equações do 2° grau:

Resolução:

Isolando x em (2):

Substituindo (3) em (1):

Como x = 5 + y:

Para y = – 2

x = 5 – 2

x = 3

Para y = – 3

x = 5 – 3

x = 2

Solução:

x = 3 e y = – 2    ou    x = 2 e y = – 3

 
3 - Resolva o sistema de equações abaixo:

Resolução:

Isolando y em (1):

Substituindo (3) em (2):

x² + y² = 100

Fazendo x² = t:

Multiplicando toda equação por t:

Como:

e

Cálculo das medidas de y:

Para

Para

Resposta:

Podemos afirmar que o sistema de equação possui quatro soluções do tipo (x, y), são elas: (6, 8), (– 6, –  8), (8, 6) e (– 8, – 6).

\frac { 5 } { 7 }

Fatorial duplo e fatorial triplo

O Fatorial de um número natural inteiro positivo é representado por n! 

n! = n⋅(n − 1)⋅(n − 2)⋅ ... ⋅3⋅2⋅1

A notação n! foi introduzida pelo matemático francês Christian Kramp em 1808, nascido em Estrasburgo, Reino da França, em 13 de maio de 1826. 

Exemplos:

Fatorial duplo:

Onde k = 1 ou 2.

Fatorial triplo:

Onde k = 1 ou 2 ou 3.

Exemplos:

Exercícios

1 - Quanto é o valor da expressão abaixo?

Resolução:

2 - Calcule:

a) 5!

b) 5!!

c) 5!!!

Resolução:

a) 5! = 5⋅4⋅3⋅2⋅1 =  120

b) 5!! =  5⋅3⋅1 = 15

c) 5!!! = 5⋅2 = 10