As Leis de Kepler descrevem o movimento dos planetas
ao redor do Sol e foram formuladas pelo astrônomo Johannes Kepler no
início do século XVII. Essas leis ajudaram a estabelecer a base da mecânica
celeste e foram essenciais para o desenvolvimento da teoria gravitacional de
Newton.
Primeira Lei: Lei das Órbitas
"Os planetas se movem em órbitas elípticas ao redor
do Sol, que ocupa um dos focos da elipse."
Isso significa que a trajetória dos planetas não é perfeitamente circular, mas
sim uma elipse, com o Sol posicionado em um dos focos.
Segunda Lei: Lei das Áreas
"A linha imaginária que liga um planeta ao Sol varre
áreas iguais em tempos iguais."
Isso implica que a velocidade orbital dos planetas não é constante; eles se
movem
Terceira Lei: lei dos
períodos ou lei da harmonia
"O quadrado do período orbital de um planeta é proporcional ao cubo do semieixo maior de sua órbita."
Matematicamente, essa relação é expressa como:
Onde:
- ( T ) é o período orbital (tempo que o planeta
leva para dar uma volta ao redor do Sol),
- ( R ) é o semieixo maior de sua órbita.
Importância das Leis de Kepler:
- Fundamentais
para a astronomia e o entendimento dos movimentos planetários.
- Essenciais
para cálculos de órbitas de satélites e sondas espaciais.
- Influenciaram
diretamente a formulação da Lei da Gravitação Universal por Newton.
Raio médio:
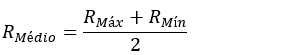
O raio médio das órbitas é medido em unidades astronômicas (ua).
Uma unidade astronômica corresponde à distância média entre a Terra e o Sol,
cerca de 1,496⋅1011 m.
1 ua = 1,496⋅1011 m
1 - (ITA 2019) Uma estação espacial, Kepler, estuda um exoplaneta cujo satélite natural tem órbita elíptica de semieixo maior a₀ e período T₀, sendo d = 32a₀ a distância entre a estação e o exoplaneta. Um objeto que se desprende de Kepler é atraído gravitacionalmente pelo exoplaneta e inicia um movimento de queda livre a partir do repouso em relação a este. Desprezando a rotação do exoplaneta, a interação gravitacional entre o satélite e o objeto, bem como as dimensões de todos os corpos envolvidos, calcule em função de T₀ o tempo de queda do objeto.
a) T = 32 To
b) T = 42 To
c) T = 22 To
d) T = 12 To
Resolução:
Vamos imaginar que o objeto estivesse em
órbita circular de raio R = 16a0 em torno do exoplaneta.
O seu período será calculado pela 3ª Lei de Kepler:
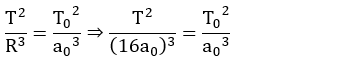




De acordo com a 3ª Lei de Kepler, o período só depende do planeta e do eixo maior da órbita. Se transformarmos a órbita circular de raio R = 16a0 numa órbita elíptica de eixo maior 32a0, o período continuaria o mesmo, T.
Neste caso, a elipse iria degenerar em um
segmento de reta e a velocidade da estação seria nula e o tempo gasto para
chegar ao exoplaneta seria a metade do período:
Logo, TQ = 32 T0
2 – (UFRGS)
Considere o raio médio da órbita de Júpiter em torno do Sol igual a 5 vezes o
raio médio da órbita da Terra. Segundo a 3ª Lei de Kepler, o
período de revolução de Júpiter em torno do Sol é de aproximadamente:
a) 5 anos.
b) 11 anos.
c) 25 anos.
d) 110
anos.
e) 125
anos.
Resolução:
Calculando
o período de revolução de Júpiter em torno do Sol por meio da fórmula da
terceira lei de Kepler que relaciona dois planetas:
Sempre que
o raio médio da órbita de um planeta estiver em unidade astronômica (ua) e o
período de revolução estiver em anos terrestres, o resultado da Lei dos
Períodos aplicada a qualquer planeta deverá ser equivalente a 1, então:


3 - A
segunda Lei de Kepler enuncia que áreas iguais são varridas pelo vetor orbital
de um planeta em intervalos de tempo iguais.
Durante 46
dias, o vetor orbital de um planeta varre 1/7 da área completa de sua órbita.
Assim, pode-se afirmar que seu período orbital é de:
a) 46
dias b) 84 dias c) 156 dias d) 276 dias e) 322 dias
Resolução:
Se 1/7 da área
é varrida em 46 dias, o período orbital completo equivale a 7/7.
Usando
regra de três:



x = 322 dias
4 - (Enem - 2009) O ônibus espacial Atlantis foi lançado ao espaço com cinco astronautas a bordo e uma câmera nova, que iria substituir uma outra danificada por um curto-circuito no telescópio Hubble. Depois de entrarem em órbita a 560 km de altura, os astronautas se aproximaram do Hubble. Dois astronautas saíram da Atlantis e se dirigiram ao telescópio. Ao abrir a porta de acesso, um deles exclamou: “Esse telescópio tem a massa grande, mas o peso é pequeno."
Considerando o texto e as leis de Kepler,
pode-se afirmar que a frase dita pelo astronauta
e) não se justifica, pois a ação da força-peso implica a ação de uma força de reação contrária, que não existe naquele ambiente. A massa do telescópio poderia ser avaliada simplesmente pelo seu volume.
Resolução:
A órbita do satélite pode ser aproximada
para um movimento circular, onde, a força exercida pela gravidade é a força
centrípeta, responsável por mantê-lo em órbita.
As leis de Kepler descrevem os movimentos
de astros menos massivos ao redor de outros mais massivos. No caso, satélite ao
redor da Terra.
Resposta: Letra D.
5 - (Enem – 2009) Na linha de uma
tradição antiga, o astrônomo grego Ptolomeu (100-170 d.C.) afirmou a tese do
geocentrismo, segundo a qual a Terra seria o centro do universo, sendo que o
Sol, a Lua e os planetas girariam em seu redor em órbitas circulares. A teoria
de Ptolomeu resolvia de modo razoável os problemas astronômicos da sua época.
Vários séculos mais tarde, o clérigo e astrônomo polonês Nicolau Copérnico
(1473-1543), ao encontrar inexatidões na teoria de Ptolomeu, formulou a teoria
do heliocentrismo, segundo a qual o Sol deveria ser considerado o centro do
universo, com a Terra, a Lua e os planetas girando circularmente em torno dele.
Por fim, o astrônomo e matemático alemão Johannes Kepler (1571- 1630), depois
de estudar o planeta Marte por cerca de trinta anos, verificou que a sua órbita
é elíptica. Esse resultado generalizou-se para os demais planetas.
A respeito dos estudiosos citados no
texto, é correto afirmar que
a) Ptolomeu apresentou as ideias mais
valiosas, por serem mais antigas e tradicionais.
b) Copérnico desenvolveu a teoria do heliocentrismo inspirado no contexto
político do Rei Sol.
c) Copérnico viveu em uma época em que a pesquisa científica era livre e
amplamente incentivada pelas autoridades.
d) Kepler estudou o planeta Marte para atender às necessidades de expansão
econômica e científica da Alemanha.
e) Kepler apresentou uma teoria científica que, graças aos métodos aplicados, pôde ser testada e generalizada.
Resposta: E
6 - (UNIFESP-SP) A Massa da Terra é aproximadamente 80 vezes a massa da Lua e a distância entre os centros de massa desses astros é aproximadamente 60 vezes o raio da Terra. A respeito do sistema Terra-Lua pode-se afirmar que:
a) a Lua gira em torno da Terra com órbita elíptica e em um dos focos dessa órbita está o centro de massa da Terra.
b) a Lua gira em torno da Terra com órbita circular e o centro de massa da Terra está no centro dessa órbita.
c) a Terra e a Lua giram em torno de um ponto comum, o centro de massa do sistema Terra-Lua, localizado no interior da Terra.
d) a Terra e a Lua giram em torno de um ponto comum, o centro de massa do sistema Terra-Lua, localizado no meio da distância entre os centros de massa da Terra e da Lua.
e) a Terra e a Lua giram em torno de um ponto comum, o centro de massa do sistema Terra-Lua, localizado no interior da Lua.
Resposta: C
7 - (Unicamp) A primeira lei de Kepler demonstrou
que os planetas se movem em órbitas elípticas e
não circulares. A segunda lei mostrou que os planetas não se movem a uma
velocidade constante. PERRY, Marvin. Civilização
Ocidental: uma história concisa. São Paulo: Martins Fontes, 1999, p.
289. (Adaptado)
É correto afirmar que as leis de Kepler:
a) confirmaram as teorias definidas por Copérnico e são exemplos
do modelo científico que passou a vigorar a partir da Alta Idade Média.
b) confirmaram as teorias defendidas por Ptolomeu e permitiram a
produção das cartas náuticas usadas no período do descobrimento da América.
c) são a base do modelo planetário geocêntrico e se tornaram as
premissas científicas que vigoram até hoje.
d) forneceram subsídios para demonstrar o modelo planetário
heliocêntrico e criticar as posições defendidas pela Igreja naquela época.
Os argumentos que eram utilizados pela Igreja para justificar o modelo geocêntrico perderam força com os modelos matemáticos das órbitas planetárias, desenvolvidas graças ao surgimento das três as leis de Kepler.
8 - (UFG) Considere que a Estação Espacial Internacional,
de massa M, descreve uma órbita elíptica estável em torno da Terra, com um
período de revolução T e raio médio R da órbita. Nesse movimento,
a) o período depende de sua massa.
b) a razão entre o cubo do seu período e o quadrado
do raio médio da órbita é uma constante de movimento.
c) o módulo de sua velocidade é constante em sua
órbita.
d) a energia mecânica total deve ser positiva.
e) a energia cinética é máxima no perigeu.
O perigeu é a posição da menor distância entre a Terra e a Estação Espacial Internacional. Nessa posição, a energia cinética é máxima e, consequentemente, a energia potencial gravitacional é mínima.
Resposta: Letra E.
I. Para a
primeira lei de Kepler (lei das órbitas), o verão ocorre quando a Terra está
mais próxima do Sol, e o inverno, quando ela está mais afastada.
II. Para a
segunda lei de Kepler (lei das áreas), a velocidade de um planeta X, em sua
órbita, diminui à medida que ele se afasta do Sol.
III. Para a
terceira lei de Kepler (lei dos períodos), o período de rotação de um planeta
em torno de seu eixo, é tanto maior quanto maior for seu período de revolução.
Com base na
análise feita, assinale a alternativa correta:
a) apenas
as proposições II e III são verdadeiras
b) apenas
as proposições I e II são verdadeiras
c) apenas a
proposição II é verdadeira
d) apenas a
proposição I é verdadeira
e) todas as
proposições são verdadeiras
Resolução:
I : As
estações do ano não têm relação com as posições de periélio e afélio.
II: VAFÉLIO <
VPERIÉLIO
III: A
terceira lei de Kepler não faz referência ao movimento de rotação do planeta.
Resposta: Letra C
10 - (UFJF) Muitas teorias sobre o Sistema Solar sucederam-se, até que, no século XVI, o polonês Nicolau Copérnico apresentou uma versão revolucionária. Para Copérnico, o Sol, e não a Terra, era o centro do Sistema. Atualmente, o modelo aceito para o Sistema Solar é, basicamente, o de Copérnico, feitas as correções propostas pelo alemão Johannes Kepler e por cientistas subsequentes.
Sobre gravitação e as leis de Kepler, considere as afirmativas, a seguir, verdadeiras (V) ou falsas (F).
I. Adotando-se o Sol como referencial, todos os planetas movem-se descrevendo órbitas elípticas, tendo o Sol como um dos focos da elipse.
II. O vetor posição do centro de massa de um planeta do Sistema Solar, em relação ao centro de massa do Sol, varre áreas iguais em intervalos de tempo iguais, não importando a posição do planeta em sua órbita.
III. O vetor posição do centro de massa de um planeta do Sistema Solar, em relação ao centro de massa do Sol, varre áreas proporcionais em intervalos de tempo iguais, não importando a posição do planeta em sua órbita.
IV. Para qualquer planeta do Sistema Solar, o quociente do cubo do raio médio da órbita pelo quadrado do período de revolução em torno do Sol é constante.
Assinale a alternativa CORRETA.
a) Todas as afirmativas são verdadeiras.
b) Apenas as afirmativas I, II e III são verdadeiras.
c) Apenas as afirmativas I, II e IV são verdadeiras.
d) Apenas as afirmativas II, III e IV são verdadeiras.
e) Apenas as afirmativas I e II são verdadeiras.
Resolução:
I. A afirmação é o próprio enunciado da primeira lei de Kepler. (Verdadeira)
II. A afirmação coincide com a definição da segunda lei de Kepler. (Verdadeira)
III. A determinação da segunda lei de Kepler, que decorre do princípio da conservação do momento angular, implica que as áreas varridas são iguais para intervalos de tempos iguais. (Falsa)
IV. A afirmativa reproduz o enunciado da terceira lei de Kepler, também conhecida como lei dos períodos. (Verdadeira)
Resposta: Letra C
11 - (Ufes) -
De acordo com uma das leis de Kepler, cada planeta completa (varre) áreas
iguais em tempos iguais em torno do Sol. Como as órbitas são elípticas e o Sol
ocupa um dos focos, conclui-se que:
I- Quando o planeta está mais próximo do Sol, sua velocidade aumenta;
II- Quando o planeta está mais distante do Sol, sua velocidade aumenta;
III-A velocidade do planeta em sua órbita elíptica independe de sua posição
relativa ao Sol.
Responda de acordo com o código a seguir:
a) somente I é correta.
b) somente
II é correta.
c) somente
II e III são corretas.
d) todas
são corretas.
e) nenhuma
é correta.
Resolução:
I – De
acordo com a primeira Lei de Kepler, a órbita dos planetas em torno do Sol é
elíptica e tem o Sol em um dos seus focos. Além disso, a excentricidade da
elipse é responsável pelo surgimento de posições particulares chamadas de periélio e afélio.
Quando os planetas aproximam-se do periélio, sua velocidade e energia cinética
aumentam. Ao se aproximarem do afélio, sua energia potencial
gravitacional aumenta, e sua velocidade orbital diminui. (Verdadeira)
II – Ao aproximar-se do
Sol, a velocidade orbital dos planetas tende a aumentar. (Falsa)
III – A
velocidade orbital do planeta depende do raio de sua órbita, portanto, depende
de sua posição relativa ao Sol. (Falsa)
Reposta: Letra
A
12 - O
modelo de universo proposto por Kepler, apesar de Heliocêntrico, tinha
disparidades com o modelo de Copérnico. Marque a alternativa que contém tais
disparidades.
a) No
modelo de Copérnico as trajetórias dos planetas eram circulares, enquanto no de
Kepler as trajetórias eram elípticas. Como sabemos hoje, as trajetórias dos
planetas ao redor do sol são elípticas.
b) No
modelo de Copérnico as trajetórias dos planetas eram elípticas, enquanto no de
Kepler as trajetórias eram circulares. Como sabemos hoje, as trajetórias dos
planetas ao redor do sol são elípticas.
c)
Copérnico acreditava que o movimento no céu era circular e uniforme. A 3ª lei
de Kepler nos mostra que o movimento dos planetas ao redor do Sol é variado.
d)
Copérnico acreditava também, de forma errada, que o movimento no céu era
circular e uniforme. A 2ª lei de Kepler nos mostra que o movimento dos planetas
ao redor do centro da galáxia é variados.
e) N.D.A
Resolução:
No modelo
de Copérnico as trajetórias dos planetas eram circulares, enquanto no de Kepler
as trajetórias eram elípticas. Como sabemos hoje, as trajetórias dos planetas
ao redor do sol são elípticas.
Reposta: Letra
A
Nenhum comentário:
Postar um comentário