No método da substituição, escolhemos uma das incógnitas e a isolamos, e substituímos na outra equação.
Exercícios:
Isolando x em (1):
x = 42 – y
Substituindo o valor de x em (2):
x – y = 8
42 – y – y = 8
42 – 2y = 8
– 2y = 8 – 42
– 2y = – 34

y = 17
Substituindo o valor de y em (1):
x + y = 42
x + 17 = 42
x = 42 – 17
x = 25
Solução: x = 25 e y = 17
2 - No sistema
o valor de x é:
a) igual a zero
b) igual a um
c) o dobro de y
d) o triplo de y
Resolução:

Isolando x em (1):

Substituindo o valor de x em (2)

-2y = 10 -20
-2y = - 10
y = - 10:(- 2)
y = 5
Substituindo o valor de y em (3):
Resposta: (d) o triplo de y.
3 - Vamos resolver o sistema de equações abaixo:

Fazendo c = 7 em m + c = 20:
m + 7 = 20
m = 20 – 7
m = 13
Solução do sistema é: c = 7 e m = 13
4 - Usando o método da substituição, resolva o sistema de equações:




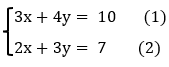
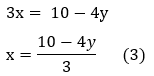



6 - Determine os valores de x e y, no sistema abaixo:

Resolução:



Resolução:
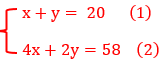






Vamos resolver esse sistema pelo método da substituição:



Substituindo o valor de “a” em:
a + b = 15
10 + b = 15
b = 15 - 10
b = 5
Substituindo o valor de “b” em:
b + c = 12
5 + c = 12
c = 12 – 5
c = 7
(a + b)⋅c
(10 + 5)⋅7





























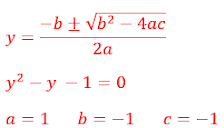


 < 0:
< 0: 







