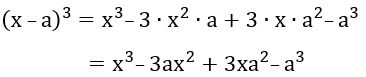Polinômios - Redução de Termos Semelhantes

 1 – (EAM – Aprendiz de marinheiro) Analise a figura a seguir: Suponha que o terreno comprado por um proprietário tenha a forma da figura acima e suas medidas sejam representadas, em unidades de comprimento, pelas variáveis X, Y e Z. A expressão algébrica que representa o perímetro desse terreno é:

                                                                    Fonte da imagem: Brasil Escola 

Lembrar que perímetro é a soma dos lados.

a) 2x + 3y + z
b) 3x + 4y + 2z
c) 3x + 3y + z
d) 3x + 2y + 3z

^Resposta: 

P = 2y + z+ x + y +x +x +y + z

P = x + x + x + 2y + y + y + z + z

P = 3x + 2y + 2y + 2z

P = 3x + 4y + 2z

2 – Para calcular a área de um retângulo, multiplicamos as medidas do comprimento com a medida da largura.

Escreva a expressão algébrica que representa a área do retângulo da figura.

                                   

a) 6x + y
b) 5xy
c) 6xy
d) 4x + 6y

 Resposta: Para b = 3y e h = 2x

A = b ⋅ h

A = 3y ⋅ 2x

A = 3 ⋅ 2 ⋅ y ⋅ x

A = 6xy

3 – Sabendo que perímetro é a soma de todos os lados de qualquer polígono, determine a expressão que representa o perímetro da figura abaixo:

a) 6x + 1
b) 12x + 2
c) 6x + 2
d) 12x + 1

Resposta: 

P = 4x + 1 +  4x + 1 + 2x + 2x

P = 4x +  4x + 2x + 2x + 1 + 1

P = 8x + 4x  + 2

P = 12x + 2

4 – Determine a expressão que representa o perímetro da figura:

Fonte da imagem - Brasil Escola.

a) 5x +12
b) 6x +12
c) 4x +12
d) 6x +9

 Resposta: P = 3x - 2 + 2x + 6 + x + 8

P = 3x - 2 + 2x + 6 + x + 8

P = 3x  + 2x +  x + 6 + 8- 2

P = 5x  +  x + 14 - 2

P = 6x + 12

Polinômio: Valor numérico

 1 – Um retângulo possui lados paralelos de medidas iguais. Então, se um lado do retângulo mede 22 cm, o lado paralelo a esse deve medir 22 cm também. Considere que a largura da figura é x. Veja a figura:

Se o perímetro, que é a soma de todos os lados do retângulo, determine o seu perímetro, para x = 8 cm.

•  44 cm
•  176 cm²
•  30 cm
•  60 cm

  Resposta: P = x + 22 + x + 22 

  P = 8 + 22 + 8 + 22 

  P = 30 + 30

  P = 60 cm

2 – Calcule o valor numérico da expressão algébrica a seguir, sabendo que x = 2 e y = 3.

Calcule o valor numérico da expressão algébrica acima

•  32
•  34
•  30
•  31

  Resposta: Para x = 2 e y = 3

  5x² + 4y = 5⋅2² + 4⋅3

  = 5⋅2⋅2 + 12

  = 10⋅2 +12

  = 20 + 12

  = 32

3 – Para calcular a área de um retângulo, multiplicamos as medidas do comprimento com a medida da largura.

Escreva a expressão algébrica que representa a área do retângulo da figura.

•  6xy
•  6x + y
•  4x + 6y
•  5xy

  Resposta: Para b = 3y e h = 2x

  A = b ⋅ h

  A = 3y ⋅ 2x

  A = 3 ⋅ 2⋅ x ⋅ y

  A = 6xy

4 – Qual deve ser o valor de k para x = 2, sabendo que o valor numérico da expressão x³ + kx − 6 seja igual a 4?

•  k = 2
•  k = 1
•  k = −1
•  k = 0

 Resposta: 

Para x = 2

x³ + kx − 6 = 4

2³ + k⋅2 − 6 = 4

2⋅ 2 ⋅ 2 + 2k − 6 = 4

8 + 2k − 6 = 4

8 + 2k = 4 + 6

8 + 2k = 10

2k = 10 − 8

2k = 2

k = 2/2

k = 1

Polinômio: Classificação e grau

 1 – Os polinômios podem ser classificados de acordo com a sua quantidade de termos. Classifique a expressão abaixo como: Monômio, Binômio, Trinômio ou Polinômio.

2x² + x – 5

•  Monômio
•  Binômio
•  Trinômio
•  Polinômio

Resposta: Trinômio e polinômio

2 – Classifique a expressão abaixo como: Monômio, Binômio, Trinômio ou Polinômio.

7x³ – 2x² + 3x – 4

•  Binômio
•  Trinômio
•  Polinômio
•  Monômio

 Resposta: Polinômio

3 – Classifique a expressão abaixo como: Monômio, Binômio, Trinômio ou Polinômio.

10x

•  Trinômio
•  Binômio
•  Monômio
•  Polinômio

 Resposta: monômio e polinômio

4 – Classifique a expressão abaixo como: Monômio, Binômio, Trinômio ou Polinômio.

4x + 7

•  Trinômio
•  Monômio
•  Binômio
•  Polinômio

 Resposta: Binômio e polinômio

5 – Dê o grau do polinômio abaixo:

10x² + 3x

•  3º
•  4º
•  2º
•  1º

 Resposta: 2º (O maior expoente da variável x)

6 – Dê o grau do polinômio abaixo:

5x + 9

•  9º
•  3º
•  1º
•  2º

 Resposta: 1º (O maior expoente da variável x é o 1, pois x¹ = x)

7 – Dê o grau do polinômio abaixo:

2x³ – 3x² + 5x – 24

•  1º
•  3º
•  4º
•  2º

 Resposta: 3º (O maior expoente da variável x é o 3)

8 – Os polinômios podem ser de dois tipos: completo ou incompleto. Classifique como: polinômio completo ou polinômio incompleto:

2x³ + 7x – 15

•  Polinômio incompleto
•  Polinômio incompleto

 Resposta: Polinômio incompleto (Faltou o expoente 2)

9 – Classifique como: polinômio completo ou polinômio incompleto:

7x³ – 2x² + 3x – 4

•  Polinômio incompleto
•  Polinômio completo

  Resposta: Polinômio completo.

10 – Classifique como: Polinômio completo ou Polinômio incompleto:

8x³ – 2x

•  Polinômio completo
•  Polinômio incompleto

  Resposta: Polinômio incompleto. (Faltou os expoentes 2 e zero)

11 – Classifique como: Polinômio completo ou polinômio incompleto:

4x + 7

•  Polinômio incompleto
•  Polinômio completo

  Resposta: Polinômio completo 

Os números naturais e a reta numérica

Você vai conhecer um pouco sobre reta numérica. Onde você pode encontrá-la no cotidiano? O termômetro é uma reta numérica, a trena também é um exemplo de reta numérica, a fita métrica é um ótimo exemplo de reta numérica além disso a régua escolar é outro exemplo de reta numérica.

1 - A casa de Amauri (A) fica na mesma rua que sua escola (E), conforme pode ser visto na representação abaixo. Qual a distância entre a casa e a escola de Amauri, em metros? a) 5 b) 10 c) 15 d) 20 Resposta: Ponto A = 10 e ponto B = 25 (25 - 10 = 15) 2 – Qual é o melhor número que pode ser representado pela letra X? a) 19 b) 17 c) 25 d) 21 Resposta: Ponto médio (18 + 24):2 = 42:2 = 21 3 – A Professora pediu a João que usasse a régua para medir o tamanho de deu lápis. Porém, a régua de João estava quebrada. Observe como ele fez. Fonte: http://www.rio.rj.gov.br/dlstatic/10112/4679740/4120195/M5_2BIM_ALUNO_2014.pdf O comprimento do lápis de João é a) 3 cm b) 5 cm c) 8 cm d) 11 cm Resposta: 8 cm - 3 cm = 5 cm 4 – Observe a posição do ponto A na reta abaixo: Fonte: http://www.rio.rj.gov.br/dlstatic/10112/4679740/4120195/M5_2BIM_ALUNO_2014.pdf O ponto A representa aproximadamente o valor na reta na numérica de: a) 170 b) 182 c) 200 d) 220 Resposta: Aproximadamente a 200.

Exercícios com juros compostos

Juros compostos é o chamado juros sobre juros. Para calcularmos os juros compostos, é conveniente calcularmos primeiro o montante.

M → Montante

C → Capital

i → Taxa 

t → Tempo

O montante é a soma do capital inicial (C) e os juros(J):

Tendo o montante e o capital, calculamos os juros compostos.

Exercícios: 

1- Um capital de R$ 1 000,00 foi emprestados durante 11 meses à taxa de 8% ao mês.

a) Qual o montante acumulado no final de 11 meses?

b) Qual o valor dos juros produzidos nesses 11 meses?

Respostas:

a) 

M = ?

C = 1 000

i = 8% = 8/100 = 0,08 

t = 11 meses

b)

    J = ?

    M = C + J

    2 331,64 = 1 000 + J

    2 331,64 – 1 000 = J

    J = R$ 331,64

    2 - Paulo aplicou R$ 12 000,00 em uma instituição financeira por um período 8 meses à  taxa de 3% ao mês.

    a) Qual o montante acumulado que Paulo vai receber no final de 8 meses?

    M = ?

    C = 12 000

    i = 3% = 3/100 = 0,03 

    t = 8 meses

    b) Qual será o valor dos juros produzidos nesses 8 meses?

    J = ?

    M = C + J

    15 201,24 = 12 000 + J

    15 201,24 – 12 000 = J

    J = R$ 3201,24

Exercícios com produtos notáveis

Produtos Notáveis são produtos de expressões algébricas que representam determinadas expressões que aparecem com muita frequência. São utilizados principalmente para a fatoração de polinômios e evitar erros com sinais.

Quadrado da soma de dois termos:

é igual ao quadrado do primeiro termo, mais duas vezes o produto do primeiro pelo segundo termo, mais o quadrado do segundo termo.

Quadrado da diferença de dois termos:

É igual ao quadrado do primeiro termo, menos duas vezes o produto do primeiro pelo segundo termo, mais o quadrado do segundo termo.

Produto da soma pela diferença:

É igual ao quadrado do primeiro termo menos o quadrado do segundo termo.

Cubo da soma:

É igual ao cubo do primeiro termo, mais três vezes o primeiro termo elevado ao quadrado vezes o segundo termo, mais três vezes o primeiro termo vezes o segundo termo elevado ao quadrado, mais o segundo termo elevado ao cubo.

Cubo da diferença:

É igual ao cubo do primeiro termo, menos três vezes o primeiro termo elevado ao quadrado vezes o segundo termo, mais três vezes o primeiro termo vezes o segundo termo elevado ao quadrado, menos o segundo termo elevado ao cubo.

Exemplos

Desafio: Sem fazer cálculos, encontre o valor de  101² - 99²:

101² - 99² = (101+99)⋅(101- 99)

101² - 99² = 200⋅2

101² - 99² = 400

Exercícios:
1 - Desenvolva as expressões algébrica (x + 1)²:

Resolução:
(x + 1)² = x² + 2 ⋅ x ⋅ 1 + 1²

= x² + 2 x + 1⋅1

= x² + 2 x + 1

2 - Desenvolva as expressões algébrica (x – 1)²:

Resolução:
(x – 1)² = x² –  2 ⋅ x ⋅ 1 + 1²

= x² – 2x + 1⋅1

= x² - 2x + 1

3 - Desenvolva as expressões algébrica (x + 1) ⋅ (x – 1):

Resolução::
(x + 1) ⋅ (x – 1) = x² – 1²

= x² – 1⋅1

= x² – 1

4 - Desenvolvendo a expressão (y + 5)², vamos obter:

a. (    ) y² + 10y + 25

b. (    ) y² + 25

c. (    ) y² + 5y + 25

d. (    ) y² + 5y + 5

Resolução:
(y + 5)² = y² + 2 ⋅ y ⋅ 5 + 5² 

             = y² + 10 ⋅ y ⋅ 1 +  5 ⋅ 5

             = y² + 10y +  25 

5 - Desenvolva a expressão (2 + h)³.

Resolução:

(2 + h)³ = 2³ + 3⋅2²⋅h + 3⋅2⋅h² + h³

 = 8 + 12h + 6h² + h³

6 - (UFPE) Se x e y são números reais distintos, então:

 e) Nenhuma das alternativas anteriores é verdadeira.

Resolução:

Resposta letra (b).

7 - Qual das alternativas abaixo é o resultado da soma entre (x + a)³ e (x – a)³?

a) 2x³ + 6xa²

b) x³ – 3x²a + 3xa² – a³

c) x³ + 3x²a + 3xa² + a³

d) 2x³ + 3xa² – 2x³ – 3xa²

e) 4x³ + 6xa²

Resolução:

Somando:

Cancelando os termos simétricos:

Resultado da soma:

8 - Simplifique a expressão abaixo:

(2x + y)² + (2x – y)² + 2  (2x – y)  (2x + y)

Resolvendo separadamente:

(2x + y)² = (2x)² + 2 (2x) y + y² = 4x² + 4xy + y²

(2x – y)² =(2x)² – 2 (2x) y + y² = 4x² – 4xy + y²

(2x – y) (2x + y) =(2x)² – y² = 4x² – y²

Então:

(2x + y)² + (2x – y)² + 2  (2x – y)  (2x + y) =

= 4x² + 4xy + y² + 4x² – 4xy + y² + 2 (4x² – y²)

= 8x² + 2y² + 8x² – 2y²

= 16x²

9 – Usando o produto notável: (a + b) ∙ (a – b) = a² – b²

Calcule:

a) 31∙ 29                                       b) 91 ∙ 89

 Resolução:

a) 31∙ 29 = (30 + 1) ∙ (30 – 1) = 30² – 1² = 900 – 1 = 899

 b) 91 ∙ 89 = (90 + 1) ∙ (90 – 1) = 90² – 1² = 8100 – 1 = 8099