Produtos Notáveis são produtos de expressões algébricas que representam determinadas expressões que aparecem com muita frequência. São utilizados principalmente para a fatoração de polinômios e evitar erros com sinais.
Quadrado da soma de dois termos:
é igual ao quadrado do primeiro termo, mais duas vezes o produto do primeiro pelo segundo termo, mais o quadrado do segundo termo.
Quadrado da diferença de dois termos:
Produto da soma pela diferença:É igual ao quadrado do primeiro termo menos o quadrado do segundo termo.
Cubo da soma:
É igual ao cubo do primeiro termo, mais três vezes o primeiro termo elevado ao quadrado vezes o segundo termo, mais três vezes o primeiro termo vezes o segundo termo elevado ao quadrado, mais o segundo termo elevado ao cubo.

Cubo da diferença:É igual ao cubo do primeiro termo, menos três vezes o primeiro termo elevado ao quadrado vezes o segundo termo, mais três vezes o primeiro termo vezes o segundo termo elevado ao quadrado, menos o segundo termo elevado ao cubo.
Exemplos
Desafio: Sem fazer cálculos, encontre o valor de 101² - 99²:
101² - 99² = (101+99)⋅(101- 99)
101² - 99² = 200⋅2
101² - 99² = 400
Exercícios:
1 - Desenvolva as expressões algébrica (x + 1)²:
Resolução:
(x + 1)² = x² + 2 ⋅ x ⋅ 1 + 1²
= x² + 2 x + 1⋅1
= x² + 2 x + 1
2 - Desenvolva as expressões algébrica (x – 1)²:
Resolução:
(x – 1)² = x² – 2 ⋅ x ⋅ 1 + 1²
= x² – 2x + 1⋅1
= x² - 2x + 1
3 - Desenvolva as expressões algébrica (x + 1) ⋅ (x – 1):
Resolução::
(x + 1) ⋅ (x – 1) = x² – 1²
= x² – 1⋅1
= x² – 14 - Desenvolvendo a
expressão (y + 5)2, vamos obter:
a. ( ) y2
+ 10y + 25
b. ( ) y2
+ 25
c. ( ) y2
+ 5y + 25
d. ( ) y2
+ 5y + 5
Resolução:
(y + 5)² = y² + 2 ⋅ y ⋅ 5 + 5² = y² + 10 ⋅ y ⋅ 1 + 5 ⋅ 5
= y² + 10y + 25
5 - Desenvolva a expressão (2 + h)³.
Resolução:
(2 + h)³ = 2³ + 3⋅2²⋅h + 3⋅2⋅h² + h³
= 8 + 12h + 6h² + h³
6 - (UFPE) Se x e y são números reais distintos, então:
e) Nenhuma das alternativas anteriores é verdadeira.
Resolução:
Resposta letra (b).
7 - Qual das
alternativas abaixo é o resultado da soma entre (x + a)3 e (x –
a)3?
a) 2x3 +
6xa2
b) x3 –
3x2a + 3xa2 – a3
c) x3 +
3x2a + 3xa2 + a3
d) 2x3 +
3xa2 – 2x3 – 3xa2
e) 4x3 +
6xa2
Resolução:
Somando:
Cancelando os termos simétricos:
Resultado da soma:
8 - Simplifique a
expressão abaixo:
(2x + y)2 + (2x – y)2 + 2
(2x –
y)
(2x +
y)
Resolvendo separadamente:
(2x + y)2 = (2x)2 + 2
(2x)
y + y2 = 4x2
+ 4xy + y2
(2x – y)2 =(2x)2 – 2
(2x)
y + y2 = 4x2
– 4xy + y2
(2x – y) (2x + y) =(2x)2 – y2
= 4x2
– y2
Então:
(2x + y)2 + (2x – y)2 + 2
(2x –
y)
(2x +
y) =
=
4x2
+ 4xy + y2 + 4x2 – 4xy
+ y2 + 2
(4x2 – y2)
=
8x2
+ 2y2 + 8x2 – 2y2
= 16x2
9
– Usando o produto notável: (a + b) ∙
(a – b) = a2 – b2
Calcule:
a)
31∙ 29 b) 91 ∙ 89
Resolução:
a) 31∙ 29 = (30 + 1) ∙
(30 – 1) = 302 – 12 = 900 – 1 = 899
b)
91 ∙ 89
= (90 + 1) ∙ (90 – 1) = 902 – 12 = 8100
– 1 = 8099







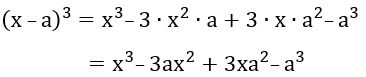




Nenhum comentário:
Postar um comentário