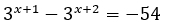

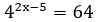
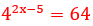





 ?
?


Como:
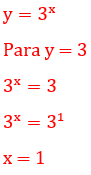

Não convém
Resposta: a solução é x = 1
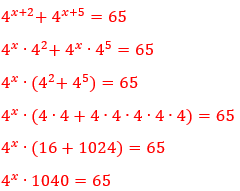

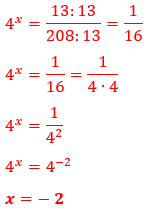
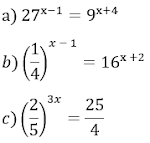







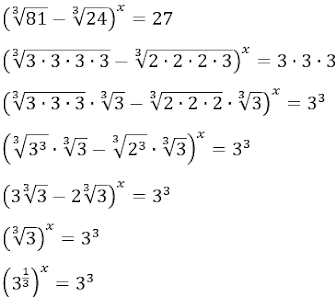


Transformando:

Fazendo:




Para y = 1







11 - Resolva a equação exponencial:








Experiências, exercícios, jogos, vídeos e textos sobre Matemática, Física, Computação e Tecnologia.
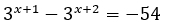

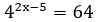
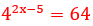





 ?
?


Como:
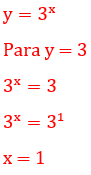

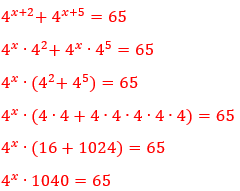

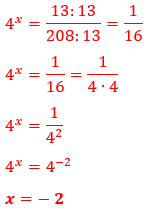
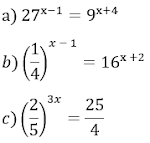







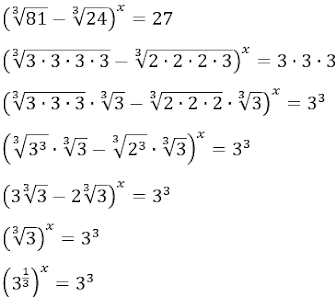


Transformando:

Fazendo:











11 - Resolva a equação exponencial:








Para calcular a área de um círculo de raio r, podemos usar a fórmula:
A = π ⋅ r²


Diferença entre o círculo e circunferência: o círculo é a área cuja fronteira é uma circunferência.



 .
.


 pertence aos números irracionais. Para a maioria dos cálculos simples é comum aproximar
pertence aos números irracionais. Para a maioria dos cálculos simples é comum aproximar  por 3,14. Uma boa parte das calculadoras científicas de 8 dígitos aproxima
por 3,14. Uma boa parte das calculadoras científicas de 8 dígitos aproxima  por 3,1415926. Para cálculos mais precisos pode-se utilizar com 52 casas decimais. Para cálculos ainda mais precisos pode-se obter aproximações de
por 3,1415926. Para cálculos mais precisos pode-se utilizar com 52 casas decimais. Para cálculos ainda mais precisos pode-se obter aproximações de  através de algoritmos computacionais.
através de algoritmos computacionais. = 3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 5923078164 06286 20899 86280 34825 34211 70679 82148 08651 32823 06647 09384 46095 50582 23172 53594 08128 48111 74502 84102 70193 85211 05559 64462 29489 54930 38196 44288 10975 66593 34461 28475 64823 37867 83165 27120 19091 45648 56692 34603 48610 45432 66482 13393 60726 02491 41273
= 3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 5923078164 06286 20899 86280 34825 34211 70679 82148 08651 32823 06647 09384 46095 50582 23172 53594 08128 48111 74502 84102 70193 85211 05559 64462 29489 54930 38196 44288 10975 66593 34461 28475 64823 37867 83165 27120 19091 45648 56692 34603 48610 45432 66482 13393 60726 02491 41273 1 - Use para π o valor 3,14 e determine o comprimento de uma circunferência quando a medida do raio é:
a) 9 cm b) 16 cm c) 0,25 m
Resolução:
a) C = ?
r = 9 cm
π = 3,14
C = 2⋅π⋅r
C = 2 ⋅ 3,14 ⋅ 9 cm
C = 6,28 ⋅ 9 cm
C = 56,52 cm
b) C = ?
r = 16 cm
π = 3,14
C = 2⋅π⋅r
C = 2 ⋅ 3,14 ⋅ 16 cm
C = 6,28 ⋅ 16 cm
C = 100,48 cm
c) C = ?
r = 0,25 m
π = 3,14
C = 2⋅π⋅r
C = 2 ⋅ 3,14 ⋅ 0,25 m
C = 6,28 ⋅ 0,25 m
C = 1,57 m

C = 50,24 cm
π = 3,14
C = 2⋅π⋅r
50,24 = 2 ⋅ 3,14 ⋅ r
50,24 = 6,28 ⋅ r

r = 8 cm



2 – Na figura, a reta t é transversal e as retas "p" e "q" são paralelas. Calcule as medidas dos ângulos assinalados.
Resolução:
4x + 30° = 3x + 40°
4x – 3x + 30° = 40°
4x – 3x = 40° – 30°
x = 10°
4x + 30° = 4⋅10° + 30° = 40° + 30° = 70°
3x + 40° = 3⋅10° + 40° = 30° + 40° = 70°
Resposta: Os ângulos assinalados medem 70° e 70°.
3 – Sabendo que r e s são retas paralelas, calcule os valores de x e y:

4x + 10° = 3x + 19°
4x – 3x = 19°– 10°
x = 9°
Os ângulos de medidas y e 3x + 19° são suplementares (soma
180°):
y + 3x +19° = 180°
y + 3 ⋅ 9°+ 19° = 180°
y + 27°+ 19° = 180°
y + 46° = 180°
y = 180°– 46°
y =134°