O estudo do sinal de uma função quadrática permite identificar em quais intervalos do domínio a função assume valores positivos, negativos ou nulos. Isso é fundamental para resolver inequações, analisar o comportamento de gráficos e tomar decisões em problemas práticos.
A função quadrática tem a forma:
f(x) = ax2 + bx + c
O que significa “sinal”:
- Positivo:
Quando f(x) > 0, o gráfico está acima do eixo x.
- Negativo:
Quando f(x) < 0, o gráfico está abaixo do eixo x.
- Zero:
Quando f(x) = 0, os pontos de interseção com o eixo x, chamados de raízes.
Como estudar o sinal:
1. Encontrar as raízes da equação f(x) = 0
Resolva a equação quadrática usando fórmula de Bhaskara ou fatoração:
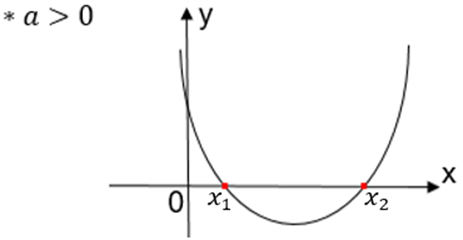

- x
< x1
- x1
< x < x2
- x
> x2
Dica Visual:
O gráfico da função quadrática é uma parábola. O
sinal da função pode ser visualizado observando em quais regiões a parábola
está acima ou abaixo do eixo x.
1º caso: △ > 0
Neste caso:A função admite dois zeros reais diferentes, x1 e x2;
A parábola que representa a função intersecta o eixo x em dois pontos.

f(x) = 0 para x = x1 ou x =
x2
f(x) > 0 para x < x1 ou x
> x2
f(x) < 0 para x1 < x < x2

f(x) = 0 para x = x1 ou x =
x2
f(x) > 0 para x1 < x < x2
f(x) < 0 para x < x1 ou x
> x2
2º caso: △ = 0
Neste caso:
A função admite dois zeros reais e iguais, x1 = x2;
A parábola que representa a função intersecta o eixo x em apenas um ponto.
f(x) = 0 para x = x1 = x2
f(x) > 0 para x ≠ x1 = x2

f(x) = 0 para x = x1 = x2
f(x) < 0 para x ≠ x1 = x2
3º caso: △ < 0
Neste caso:
A função não admite zeros reais;
A parábola que representa a função não intersecta o eixo x.

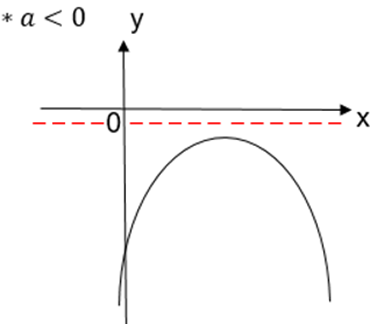
f(x) < 0, ∀ x ∈ ℝ
Exemplos
1 – Estudar o sinal da função f(x) = x2 – 4.
Resolução:
Para encontrar as raízes de f(x), vamos usar fatoração:
f(x) = 0 ⇒ x2
x2 – 22
ou
Raízes: x = – 2 e x = 2

- A
parábola tem concavidade voltada para cima: a > 0
- Sinal:
- f(x)
> 0 quando x < – 2 ou x > 2
- f(x)
< 0 quando – 2 < x < 2
- f(x)
= 0 quando x = – 2 ou x = 2
2 – Estudar o sinal da função f(x) = x² – 5x + 6.
Resolução:
Fazendo f(x) = 0:
x² – 5x + 6 = 0
a = 1, b = – 5 e c = 6
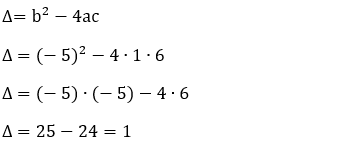

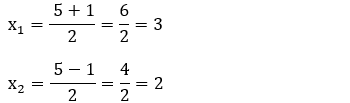
Concavidade:
Sinal:

Antes da raiz 2 e depois da raiz 3, a função é positiva (f(x) > 0).
Nos pontos x = 2 e x = 3, a função é nula (f(x) = 0).
Exercícios
1 - Estude o sinal da função f(x) = x2 – 2x + 1.
Resolução:
Fazendo f(x) = 0:
x2 – 2x + 1 = 0
a = 1, b = – 2 e c = 1
Raízes:
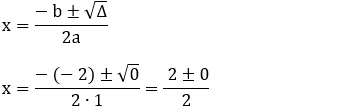

A parábola tem concavidade voltada para cima: a = 1 > 0
Sinais:
f(x) = 0 para x = 1
f(x) > 0 para x ≠ 1
2 - Faça o estudo do sinal da função f(x) = 6x2 – 5x + 1.
Resolução:
Fazendo f(x) = 0:
x2 – 2x + 1 = 0
a = 6, b = – 5 e c = 1
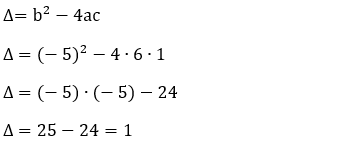
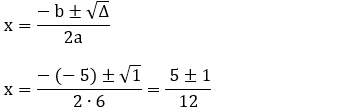

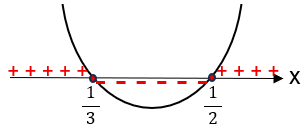
f(x) > 0 quando:
3 - Estude o sinal da função f(x) = – x2 – 2x + 3.
Resolução:
Fazendo f(x) = 0:
– x2 – 2x + 3 = 0
a = – 1, b = – 2 e c = 3
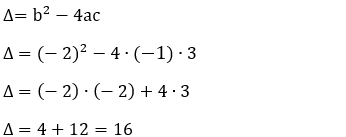
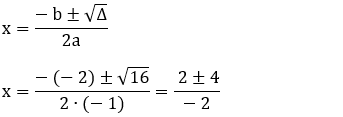

A parábola tem concavidade voltada para baixo: a = – 1 < 0

Sinais:
f(x)
> 0 quando – 3 < x < 1
f(x)
< 0 quando x < – 3 ou x > 1
f(x)
= 0 quando x = – 3 ou x = 1
4 - Dada a função f(x) = x2 + 4x + 4, faça o estudo de seu
sinal.
Resolução:
Fazendo f(x) = 0:
x2 + 4x + 4 = 0
a = 1, b = 4 e c = 4

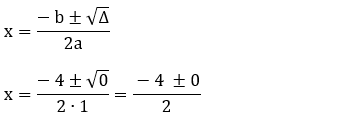


f(x) = 0 para x = – 2
f(x) > 0 para x ≠ – 2
5 – Fazer o estudo do sinal da função f(x) = x(1 – x) – 1.
Resolução:
f(x) = x(1 – x) – 1
f(x) = x – x2 – 1
f(x) = – x2 + x – 1
Fazendo f(x) = 0:
– x2 + x – 1 = 0
a = – 1, b = 1 e c = – 1

A parábola tem concavidade voltada para baixo: a = – 1 <
0

6 - Determine os valores de c para os quais temos 𝑥2 + 4𝑥 + 𝑐 > 0, ∀ 𝑥 ∈ ℝ.
Resolução:Condição: △ < 0
a = 1, b = 4 e c = ?

Multiplicado por ( – 1):
– 4c < –16 ⋅ ( –
1)
4c > 16


Nenhum comentário:
Postar um comentário