As alavancas são máquinas simples que ajudam a
multiplicar forças, permitindo levantar, mover ou equilibrar objetos com mais
facilidade. Elas funcionam com base no princípio da alavanca, formulado
por Arquimedes, que dizia:
"Dê-me uma alavanca e um ponto de apoio, e moverei o
mundo."
Estrutura de Uma Alavanca
Uma alavanca possui três elementos principais:
- Ponto
de apoio (fulcro): Onde a alavanca gira.
- Força
motora (esforço): A força aplicada pelo usuário.
- Resistência
(carga): O peso ou força que se deseja mover.
Elas são classificadas de acordo com a posição relativa
desses três elementos:
|
Tipo de
Alavanca |
Exemplo |
Ordem dos
elementos |
|
1ª Classe |
Tesoura,
gangorra |
Apoio entre
força e carga |
|
2ª Classe |
Carrinho de
mão |
Carga entre
apoio e força |
|
3ª Classe |
Pinça, braço
humano |
Força entre
apoio e carga |
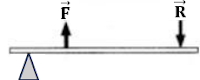
Primeira Classe (Alavanca interfixa)
A alavanca interfixa é aquela em que o
ponto de apoio se localiza entre a força potente e a força resistente, como
demonstrado na imagem abaixo:

Segunda Classe (Alavanca inter-resistente)
A alavanca inter-resistente é aquela em que a força resistente se localiza entre a força potente e o ponto de apoio, como demonstrado na imagem abaixo:

Terceira Classe (Alavanca interpotente)
A alavanca interpotente é aquela em que a força potente se localiza entre a força resistente e o ponto de apoio, como demonstrado na imagem abaixo:
Princípio Físico
O estudo das alavancas envolve o momento de força
(torque):
Onde:
- ( M
) é o momento de força (torque),
- ( F
) é a força aplicada,
- ( d
) é a distância do ponto de apoio.
A condição de equilíbrio ocorre quando o somatório dos
momentos em relação ao ponto de apoio é zero.
Fórmula da alavanca
Fp ∙ dp = Fr ∙ dr
- (Fp) força
potente, medida em Newton [N].
- (dp) distância
da força potente, medida em metros [m].
- (Fr)
força resistente, medida em Newton [N].
- (dr) distância
da força resistente, medida em metros [m].
Aplicações no Cotidiano
As alavancas estão em todo lugar:
- Ferramentas
(abridor de garrafa, pé de cabra);
- Esportes
(raquetes, tacos);
- Biomecânica
(movimento dos membros humanos);
- Engenharia
(mecanismos de içamento e alavancagem).
Exercícios
1 – (UFRGS) A barra da figura é um corpo rígido de peso desprezível, apoiada no ponto P.

Qual o módulo da força F que mantém a barra em equilíbrio mecânico na posição horizontal?
A) 10 N
B) 20 N
C) 30 N
D) 40 N
E) 60 N
Resolução:
d = 60 cm
d1 = 30 cm
F1 = 20 N
F =?
F ⋅ d = F1 ⋅ d1
F⋅ 60 = 20 ⋅ 30
F⋅ 60 = 600
F = 10 N
2 – (Encceja) A imagem representa uma balança utilizada para a medida da massa de uma fruta. A massa colocada no prato direito da balança é de 100 g e o sistema encontra-se em equilíbrio.

A massa dessa fruta, em grama, é:
A) 100
B) 120
C) 500
D) 600
Resolução:
d1 = 10 cm
d2 = 50 cm
m1 = ?
m2 = 100 g
F1 = P1 = m1 ⋅ g
F2 = P2 = m2 ⋅ g
Substituindo esses valores em:
F1 ⋅ d1 = F2 ⋅ d2

m1 = 500 g
3 – (Enem) Em um experimento, um professor levou para a sala
de aula um saco de arroz, um pedaço de madeira triangular e uma barra de ferro
cilíndrica e homogênea. Ele propôs que fizessem a medição da massa da barra
utilizando esses objetos. Para isso, os alunos fizeram marcações na barra,
dividindo-a em oito partes iguais, e em seguida apoiaram-na sobre a base
triangular, com o saco de arroz pendurado em uma de suas extremidades, até
atingir a situação de equilíbrio.

Nessa situação, qual foi a massa da barra obtida pelos
alunos?
A) 3,00 kg
B) 3,75 kg
C) 5,00 kg
D) 6,00 kg
E) 15,00 kg
Resolução:
O peso da barra está no seu centro de massa:

dA = 3 unidades
dB = 1 unidade
mA = 5 kg
mB =?
FB ⋅ dB = FA ⋅ dA
PB ⋅ dB = PA ⋅ dA
mB ⋅ g ⋅ dB = mA ⋅ g ⋅ dA
mB = 15 kg
4 – (UFRGS) Na figura, o segmento AB representa uma barra
homogênea, de 1m de comprimento, que é mantida em equilíbrio mecânico na
posição horizontal. A barra está apoiada num ponto a 25 cm da extremidade A, e
o módulo da força F, aplicada na extremidade B, é 2 N. Qual é o peso da barra?

(A) 0,66 N (B) 1 N
(C) 4 N (D) 6 N
(E) 8 N
Resolução:
O peso da barra está no seu centro de massa:

dP = 25 cm
dB = 75 cm
FB = F = 2 N
P =?
FP = P
FP⋅ dP = FB⋅ dB
P⋅ dP = FB⋅ dB
5 – (ACAFE - Medicina 2016/2) Basicamente, uma alavanca é uma barra que pode girar em torno de um ponto de apoio, chamado de polo. Mesmo no nosso corpo existem muitas alavancas, já que existem muitas partes articuláveis.
Na figura a seguir
vemos o exemplo de três tipos alavancas diferentes: no pé (1), no
braço/antebraço (2) e na cabeça (3).

A alternativa
correta que mostra na sequência (1), (2) e (3) a classificação conforme a
posição do ponto de apoio em relação às forças aplicadas é:
A) interfixa;
interpotente e inter-resistente.
B)
inter-resistente; interfixa e interpotente.
C) interpotente;
interfixa e inter-resistente.
D)
inter-resistente; interpotente e interfixa.
Resolução:
No pé tem alavanca
inter-resistente, já que a força resistente está entre a força potente e o
ponto de apoio. No braço tem alavanca interpotente, já que a força potente está
entre a força resistente e o ponto de apoio. Na cabeça tem alavanca interfixa,
já que o ponto de apoio está entre a força potente e a força resistente.
Resposta: Letra D
6 – (Uece) Uma gangorra em um parquinho infantil é ocupada por dois gêmeos idênticos e de mesma massa, Cosmo e Damião. Na brincadeira, enquanto um dos irmãos sobe em um dos acentos do brinquedo, o outro desce no outro acento. O brinquedo pode ser descrito como uma haste rígida, com um acento em cada extremidade, e livre para girar em um plano vertical em torno do ponto central. Considere os torques na haste da gangorra exercidos pelas forças peso de Cosmo (τc) e de Damião (τd), em relação ao ponto central. Na configuração em que Cosmo está na posição mais alta, é correto afirmar que
a) |τc|
< |τd|.
b) |τc|
= |τd|.
c) |τc|
> |τd|.
d) |τc|
> –|τd|.
Resolução:
Como as crianças possuem mesma massa, o que lhes garante mesmo peso, e
estão posicionadas na mesma distância em relação ao eixo de rotação da
gangorra, os torques gerados pelos irmãos devem ser iguais.
Resposta: Letra B
7 – (Udesc) Ao se fechar uma porta, aplica-se uma força na maçaneta para ela rotacionar em torno de um eixo fixo onde estão as dobradiças. Com relação ao movimento dessa porta, analise as proposições.
I. Quanto maior a
distância perpendicular entre a maçaneta e as dobradiças, menos efetivo é o
torque da força.
II. A unidade do torque da força no Sl é o N⋅m, podendo também ser medida em Joule (J).
III. O torque da
força depende da distância perpendicular entre a maçaneta e as dobradiças.
IV. Qualquer que
seja a direção da força, o seu torque será não nulo, consequentemente, a porta
rotacionará sempre.
Assinale a
alternativa correta:
a) Somente a
afirmativa II é verdadeira.
b) Somente as
afirmativas I e II são verdadeiras.
c) Somente a
afirmativa IV é verdadeira.
d) Somente a
afirmativa III é verdadeira.
e) Somente as
afirmativas II e III são verdadeiras.
Resolução:
I – Falsa. Quanto
maior é a distância perpendicular entre a maçaneta e as dobradiças, mais
efetivo é o torque da força.
II – Falsa. O
torque não é uma quantidade de energia, por isso, não pode ser determinado em
joule (J).
III – Correta.
IV – Falsa. Para a
determinação do torque, são consideradas somente forças perpendiculares a um
sistema de rotação.
Resposta: Letra D
Nenhum comentário:
Postar um comentário