Valor máximo e valor mínimo de uma função quadrática

O estudo de valores máximo e mínimo em funções quadráticas é um dos pilares da análise matemática, especialmente útil em problemas de otimização, gráficos e modelagem de situações reais. As funções quadráticas têm a forma geral:

f(x) = ax² + bx + c

Características da função quadrática:

• O gráfico dessa função é uma parábola.
• Se ( a > 0 ), a parábola é voltada para cima e possui um mínimo.
• Se ( a < 0 ), a parábola é voltada para baixo e possui um máximo.
• O valor máximo ou mínimo ocorre no vértice da parábola.

a > 0

a < 0

Coordenadas do Vértice

As coordenadas do vértice de uma função quadrática, dada por f(x) = ax² + bx +c, podem ser encontradas através das seguintes fórmulas:

Sendo:

O valor y_v representa o valor mínimo ou máximo da função.

Exemplos:

1 - Dada a função f(x) = 2x² – 4x + 1, calcule seu valor máximo ou mínimo.

Resolução:

a = 2, b = – 4 e c = 1

Como a > 0 então a parábola tem mínimo.

Cálculo da abscissa do vértice:

Cálculo do valor mínimo: 

Resposta: O mínimo da função é y_{v =} – 1 e ocorre no ponto V(1, – 1).

 2 - Determine o vértice da função f(x) = – x² – 2x + 3 e diga se ele é ponto de máximo ou de mínimo.

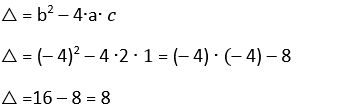
Resolução:

a = – 1, b = – 2 e c = 3

Cálculo da abscissa do vértice:

Cálculo da ordenada do vértice:

△ = b² – 4⋅ a⋅ c   

△ = (– 2)² – 4 ⋅(– 1)⋅3 = (– 2)⋅(– 2) + 4⋅3

△ = 4 + 12 = 16

Resposta: Como a < 0 então a parábola tem máximo e o vértice ocorre no ponto V(– 1, 4).

Exercícios

1 – O lucro de uma fábrica na venda de determinado produto é dado pela função L(x) = – 5x² + 100x – 80, onde x representa o número de produtos vendidos e L(x) é o lucro em reais. Determine:

a) O lucro máximo obtido pela fábrica na venda desses produtos.
b) Quantos produtos precisam ser vendidos para obtenção do lucro máximo.

Resolução:

a) a = – 5, b = 100 e c = – 80

Como a < 0, a parábola terá um ponto máximo:

△ = b² – 4⋅ a⋅ c     

△ = 100² – 4⋅(– 5)⋅( – 80)

△ = 100⋅100 + 20⋅ (– 80)

△ = 10 000 – 1 600 = 8 400

Resposta: O lucro máximo da fábrica será de R$ 420,00.

b) O número de produtos a serem vendidos para obtenção do lucro máximo será dado pelo X_v: 

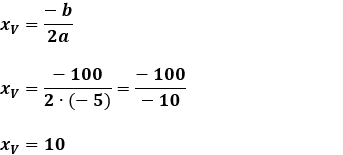
Resposta: A fábrica precisa vender 10 produtos para obter o lucro máximo desejado.

2 – (UA–AM, adaptado) Após várias experiências em laboratório, observou-se que a concentração de certo antibiótico no sangue de cobaias, varia de acordo com a função f(x) = 12x – 2x², em que x é o tempo decorrido, em horas, após a ingestão do antibiótico. Nessas condições, determine:

a) o valor máximo da concentração do antibiótico no sangue das cobaias.

b) O tempo necessário para que o antibiótico atinja nível máximo de concentração no sangue dessas cobaias. 

c) Uma nova dose do antibiótico deverá ser aplicada no sangue destas cobaias quando o nível de concentração seja nulo. Depois de quanto tempo essa nova dose será aplicada?

d) A concentração de antibiótico no sangue das cobaias, nas primeiras 6 horas de experiência, calculando de hora em hora.

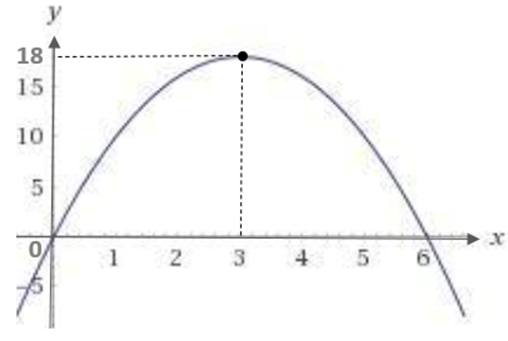
e) Faça um esboço do gráfico da função que representa esta situação.

Resolução:

a) a = – 2,  b = 12   e   c = 0

Como a < 0, a parábola do gráfico de f(x) terá um ponto máximo:

△ = b² – 4⋅ a⋅ c    

△ = 12² – 4⋅ (– 2)⋅ 0

△ = 12⋅12 + 8⋅0

△ = 144 + 0 = 144

y_{v = 18}

Resposta: O valor máximo da concentração do antibiótico no sangue das cobaias é 18.

b)

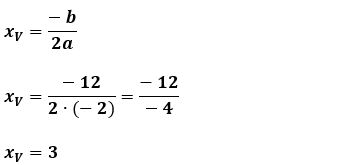
Resposta: 3 horas

c) f(x) = 12x – 2x²

f(x) = 0

12x – 2x² = 0

Colocando 2x em evidência:

12x – 2x² = 0

2x⋅ (6 – x) = 0 ⇒ 6 – x = 0 ∴ x = 6

Resposta: Depois de 6 horas.

d) x = 0; y = 0

x = 1; y = 12⋅ (1) – 2⋅ (1)² = 10

x = 2; y = 12⋅ (2) – 2⋅ (2)² = 16

x = 3; y = 12⋅ (3) – 2⋅ (3)² = 18

x = 4; y = 12⋅ (4) – 2⋅ (4)² = 16

x = 5; y = 12⋅ (5) – 2⋅ (5)² = 10

x = 6; y = 12⋅ (6) – 2⋅ (6)² = 0

e) 

3 – Uma empresa fabrica chapéus e o lucro L, em milhares de reais, é dado pela função L(x) = – 2x² + 16x – 7, em que x é a quantidade de chapéus produzidos. Qual é o lucro máximo que essa empresa pode alcançar?

a) R$ 25,00

b) R$ 4,00

c) R$ 25 000,00

d) R$ 4 000,00

Resolução:                          

a = – 2, b = 16 e c = – 7

Como a < 0, a parábola de L(x) terá um ponto máximo:

△ = b² – 4⋅a⋅c     

△ = 16² – 4⋅(–2)⋅( – 7)

△ = 16 ⋅16 + 8⋅( – 7)

△ = 256 – 56 = 200

L(x) = y

Y_V = 25 mil = 25 000

Resposta: O lucro máximo da fábrica será de R$ 25 000,00.

4 – Uma função real f(x), dada por f(x) = – x² + 4x + 6, tem um valor:

a) mínimo, no valor de 2, para x = 1

b) máximo, no valor de 8, para x = – 1

c) mínimo, no valor de – 12, para x = – 2

d) máximo, no valor de 10, para x = 2

e) máximo, no valor de 8, para x = 2

Resolução:

a = – 1, b = 4 e c = 6

Como a < 0, a parábola de f(x) terá um ponto máximo:

△ = b² – 4⋅ a⋅c     

△ = 4² – 4⋅(–1)⋅6

△ = 4⋅4 + 4⋅6

△ = 16 + 24 = 40

f(x) = y

Y_V = 10

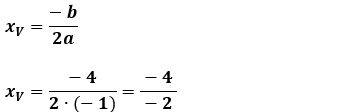
x_V = 2

Resposta: Letra D.

5 – Determine o valor de k de modo que o valor mínimo da função f(x) = (k – 1)x² + 6x – 2 seja – 5.

Resolução:

Condição: a > 0 e y_V = – 5.

a = k – 1,  b = 6   e   c = – 2

k – 1 > 0     ⇒     k >1

△ = b² – 4⋅a⋅c     

△ = 6² – 4⋅ (k – 1) ⋅ (– 2)

△ = 6⋅6 – 4(– 2k + 2)

△ = 36 + 8k – 8 = 8k + 28 

– 8k – 28 = – 5(4k – 4)

 – 8k – 28 = – 20k  + 20

20k – 8k = 20 + 28

12k = 48

k = 4 (Satisfaz a condição k > 1)

Logo, para que o valor mínimo de f(x) seja – 5, temos que ter k = 4.

6 – Determine m de modo que a função f(x) = – 4x² + (m +1)x + 2 tenha valor máximo para x = 2.

Resolução:

a = – 4,     b = m + 1     e     c = 2

x_V = 2

– m – 1 = – 16    – m = – 16 + 1 

– m = – 15   ⇒   m = 15 

 Logo, a função f(x)tem valor máximo para x = 2 quando m = 15.