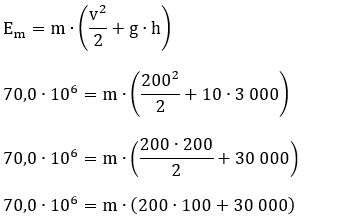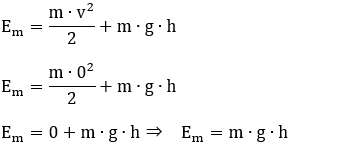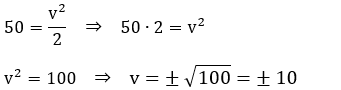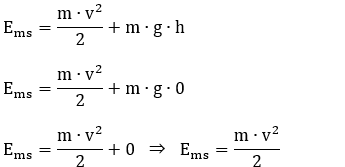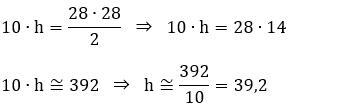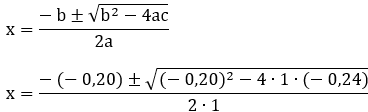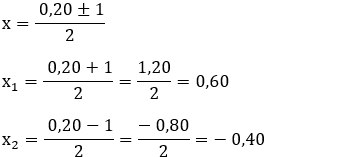A força elástica é a força que surge quando um corpo elástico - como uma mola, borracha ou elástico - sofre uma deformação (compressão ou alongamento) e tende a retornar à sua forma original. Ela é uma força restauradora, ou seja, sempre atua no sentido contrário à deformação.
O estudo da força elástica está diretamente relacionado à Lei
de Hooke, formulada pelo cientista britânico Robert Hooke no século
XVII. A lei afirma que:
F = k⋅x
Onde:
- ( F
) é a força elástica (em newtons),
- ( k
) é a constante elástica (depende do material e da rigidez da mola),
- ( x
) é a deformação sofrida (em metros), medida a partir da posição de
equilíbrio.
A força elástica está por toda parte: Aqui vão alguns
exemplos:
- Molas
em balanças, amortecedores e brinquedos;
- Cintos
de segurança, que esticam e seguram com base nesse princípio;
- Arcos
e catapultas, usados desde a Antiguidade;
- Aparelhos
ortodônticos, que utilizam forças elásticas para alinhar os dentes;
- Próteses
e biomecânica, no estudo dos movimentos e resistências articulares.
Associação de molas
Ao fazer a associação de molas, podemos calcular o
valor do coeficiente de elasticidade equivalente, ou seja, no lugar das molas
de k1 e k2, poderíamos simplesmente colocar uma mola de keq

Duas molas em paralelo:

1 - Sabendo que a constante elástica de uma mola é igual a 350 N/m, determine qual é a força necessária para que essa mola sofra uma deformação de 2,0 cm.
b) 12 N
c) 7 N
d) 70 N
e) 35 N
Resolução:
k = 350 N/m
F = 2,0 kN = 2 000 N
F = k⋅x
F = 350⋅0,02
F = 7 N
b) 5,0 N
c) 100 N
d) 50 N
e) 0,05 N
2 000 = k⋅0,025
k = 80 000 N/m ou k = 80 kN/m
3 – (UEL) Uma mola,
submetida à ação de uma força de intensidade 10 N , está
deformada de 2,0 cm . O módulo do trabalho realizado pela
força elástica na deformação de 0 a 2,0 cm foi, em
joules, de:
A) 0,1.
B) 0,2.
C) 0,5.
D) 1,0.
E) 2,0.
Resolução:
F = 10 N
x = 2 cm = 2:100 m = 0,02 m
F = k⋅x
10 = k⋅0,02
k = 500 N/m

𝝉 = 0,1 J
4 – (UFSM) Durante os exercícios de força realizados por um
corredor, é usada uma tira de borracha presa ao seu abdome. Nos arranques, o
atleta obtém os seguintes resultados:

Δx é a elongação da tira. O máximo de força atingido
pelo atleta, sabendo que a constante elástica da tira é de 300 N/m e que
obedece à lei de Hooke, é, em N:
a) 23 520
b) 17 600
c) 1 760
d) 840
e) 84
Resolução:
k = 300 N/m
Fel
Fel = 300⋅0,28
Fel = 84 N
Exercícios
1 – (UFG) Para proteção e conforto, os tênis modernos são equipados com amortecedores constituídos de molas. Após sair da aula de física experimental e olhar para o tênis de seu amigo, você verificou que ele estava com um determinado modelo que possui três molas idênticas, e essas molas são associadas em paralelo e simetricamente. Elas sofrem uma deformação de 4 mm quando o tênis é calçado por uma pessoa de 84 kg. Considerando que essa pessoa permaneça parada, a constante elástica das molas será, em kN/m, de (considere g = 10m/s²):
a) 35,0 kN/m.
b) 105,0 kN/m.
c) 157,5 kN/m.
d) 70,0 kN/m.
e) 210,0 kN/m.
Resolução:
Força (Peso): A força devido ao peso da pessoa é:
F = m ⋅ g
F = 84⋅10
F = 840 N
Para cada perna:
840 N:2 = 420 N
Havendo 3 molas em cada tênis, cada mola,
individualmente, sustenta:
420 N:3 = 140 N
Deformação:
k = 4 mm = 4:1 000 m = 0,004 m
F = k⋅x
140 = k⋅0,004
k = 35⋅1 000 N/m ou 35 kN/m
k = 35 k
k = 35 kN/m
2 – (Mack) O conjunto mostrado está em movimento devido à ação da força horizontal de 50 N. Despreze os atritos. O coeficiente de elasticidade da mola ideal que está entre os blocos A e B, de massas respectivamente iguais a 6 kg e 4 kg, é 1 000 N/m. A deformação sofrida pela mola é:

a) 2 cm
b) 4 cm
c) 5 cm
d) 7 cm
e) 10 cm
Resolução:
mA = 6 kg
mB = 4 kg
FR = 50 N
K = 1 000 N/m
Cálculo da aceleração do sistema, através da fórmula da
força resultante:
FR = m⋅a
A massa é dada em termos do somatório das massas dos dois
blocos:
FR = (mA + mB)⋅a
50 = (6 + 4)⋅a
50 = 10⋅a
a = 5 m/s2
Cálculo da deformação sofrida pela mola no bloco A, através
da fórmula da força resultante e da força elástica:
FR = m⋅a
Como a única força atuando sobre o bloco é a força elástica,
então:
Fel = k ⋅ x
Fel = mA ⋅ a
k ⋅ x = mA ⋅ a
1 000 ⋅ x = 4 ⋅ 5x = 0,02 m
x = 2 cm
3 - (UFU-MG) O tiro com arco é um esporte olímpico desde a realização da segunda olimpíada em Paris, no ano de 1900. O arco é um dispositivo que converte energia potencial elástica, armazenada quando a corda do arco é tensionada, em energia cinética, que é transferida para a flecha.


O valor e unidades da constante elástica, k, do arco são:
a) 16 m/N
b) 1,6 kN/m
c) 35 N/m
d) 5/8 x 10-2 m/N
Resolução:
Como esses valores são proporcionais, podemos escolher qualquer par (F, x):
Para F = 160 N, x = 10 cm
x = 10 cm = 10:100 m = 0,1 m
F = k⋅x
k = 1 600 N/m
k = 1,6 kN/m
Resolução:
x = 0,25 m
k = 5 000 N/m
m = 75 kg
F = P
P = m⋅g
F = k⋅x


x = 0,15 m
Nós agora subtraímos isto do comprimento nominal da mola:
L = L0 – x
L = 0,25 – 0,15
L = 0,1 m
5 - (FUND. CARLOS CHAGAS) Uma mola elástica ideal, submetida a ação de uma força de intensidade F = 10N, está deformada de 2,0 cm. A energia elástica armazenada na mola é de:
a) 0,10 J
b) 0,20 J
c) 0,50 J
d) 1,0 J
e) 2,0 J
Resolução:
Cálculo da constante elástica da mola (Lei de Hooke):
F = 10 N
X = 2 cm = 2:100 m = 0,02 m
F = k⋅x
10 = k⋅0,02
K = 500 N/m
Calculo da energia potencial elástica:

Epe = 0,1 J
6 - Duas molas A e B de comprimentos iguais a L, mas de constantes elásticas diferentes (KA = 0,2 KB), são unidas no ponto C e alongadas até o comprimento total 4L. Os terminais das molas são então fixados em suportes rígidos, como mostra a figura. Determine a razão, LA/LB entre os comprimentos das molas nessa situação.

Resolução:
A força
elástica na mola A é:
FA = KA⋅(LA − L)
A força
elástica na mola B é:
FB = KB⋅(LB − L)
Como as molas estão em equilíbrio e unidas, 𝐹𝐴 = 𝐹𝐵:
KA⋅(LA − L) = KB⋅(LB − L)
Como: KA
= 0,2KB
0,2KB⋅(LB – L) = KB⋅(LB – L)
0,2⋅(LA – L) = LB – L
O comprimento total é:
LA + LB = 4L ⇒ LB = 4L − LA
Substituindo LB em:
0,2⋅(LA – L) = LB – L
0,2⋅(LA – L) = 4L − LA – L
0,2LA – 0,2L = 3L − LA
0,2LA + LA = 3L + 0,2L
1,2LA = 3,2L
O comprimento total é:
LA + LB = 4L ⇒ LB = 4L − LA
Substituindo LB em:
0,2⋅(LA – L) = LB – L
0,2⋅(LA – L) = 4L − LA – L
0,2LA – 0,2L = 3L − LA
0,2LA + LA = 3L + 0,2L
1,2LA = 3,2L
Como LB = 4L − LA



Logo:
Comparando-se as constantes elásticas destas 3 molas, tem-se que

a) K1 > K2 > K3.
b) K2 > K1 > K3.
c) K2 > K3 > K1.
d) K3 > K2 > K1.
Resolução:
Aplicando a Lei de Hooke para força e deformação elástica, podemos isolar o K da constante elástica.
( ) A expressão da força que distende a mola de constante k é F = k∙x, onde x é o alongamento da mola.
( ) A mola do item anterior reage sempre com força F′ = − k∙x, onde x é o alongamento da mola.
( ) Os dinamômetros são equipamentos destinados a medir forças.
( ) Nos sistemas conservativos, a energia mecânica é conservada.
Todas as alternativas são verdadeiras.