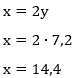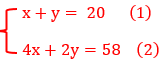Exercícios com média aritmética

1 - Qual é a média aritmética simples dos números 12, 8 e 13?
a) 9
b) 10,4
c) 11
d) 9,3

Resolução:

2 - Os jogadores de uma equipe de basquete apresentam as seguintes idades: 28, 29, 19, 23 e 21 anos. Qual a média de idade desta equipe?

Resolução:

Resposta: A média de idade desta equipe é de 24 anos.

3 - Em um grupo de seis amigos, foram computadas suas idades. Determine qual a idade média desse grupo.

Nomes	Idades (anos)
Paulo	12
Carlos	13
André	15
Roberto	17
José	19
Pedro	20

Resolução:

Resposta: A média de idade desse grupo é de 16 anos.

4 - João deseja calcular a média aritmética das notas que tirou em matemática. Calcule a média de suas notas em matemática.

Matemática
1ª prova	8,6
2ª prova	9,3
3ª prova	9,7
4ª prova	10,0

a) 9,4
b) 8,9
c) 9,3
d) 9,8

Resolução:

5 - (PUC-RIO) – As notas de uma turma de alunos no teste de matemática foram 10, 10, 9, 8, 8, 8, 7, 7, 4 e 2. Qual a média da turma?

a) 7,8
b) 8,2
c) 7,3
d) 8,0

Resolução:

6 - O dólar é considerado uma moeda de troca internacional, por isso, o seu valor diário possui variações. Acompanhando a variação de preços do dólar em reais durante uma semana, foram verificadas estas variações:

Segunda feira	Terça feira	Quarta feira	Quinta feira	Sexta feira
R$ 5,20	R$ 5,40	R$ 5,30	R$ 5,50	R$ 5,80

Determine o valor médio do preço do dólar nessa semana.

a) R$ 5,66
b) R$ 5,44
c) R$ 5,34
d) R$ 5,52

Resolução:

7 - A média aritmética entre dois números é 50 e um dos números e 35 qual é o outro número?

Resolução:

Resposta: o outro número é 65.

8 - (AGENTE-ADM) A média aritmética das idades de 10 alunos de uma determinada turma é igual a 15 anos. Se dois alunos, um com 12 anos e o outro com 18 anos, saírem dessa turma, a media aritmética das idades dos 8 alunos restantes será igual a:

a) 13 anos

b) 14 anos

c) 15 anos

d) 16 anos

Resolução:

Média aritmética das idades de 10 alunos:

Média aritmética das idades de 8 alunos:

9 - (VUNESP) A média das idades de 3 irmãos é 20 anos. Sabe-se que os 2 irmãos mais velhos são gêmeos e têm 21 anos de idade. Então, a idade do irmão mais novo é:

a) 16 anos

b) 17 anos

c) 18 anos

d) 19 anos

Resolução:

Resposta: O irmão mais novo tem 18 anos.

Problemas com sistema de equações do 1º grau

 1 - A distância do ponto A ao ponto B é 29 cm. Sabendo que x – y = 6,5, qual é o valor de y?

Resolução:
3x + y + 2x + y = 29
5x + 2y = 29
Resolvendo o sistema de equações:

Isolando x em (2):

x = 6,5 + y

Substituindo o valor de x em (1):

2 - A soma de um número mais a metade de outro é igual a 18. Sabe-se que o primeiro é o dobro do segundo. Quais são esses números?

Resolução:

Primeiramente vamos escrever o sistema que representa o problema:

Substituindo (2) em (1): 

Substituindo y em (2):

Resposta: Estes números são 7,2 e 14,4.

3 - A soma de um número x com o dobro de um número y é – 7; e a diferença entre o triplo desse número x e número y é igual a 7. Sendo assim, determine: 

a) os valores de x e y; 

b) o valor do produto de x e y. 

Resolução: 

a) Primeiramente vamos escrever o sistema de equações que representa esse problema:

Isolando x em (1):

Substituindo o valor de x em (2):

Substituindo o valor de y em (3):

Resposta: x = 1 e y = - 4 

4 - Um senhor tem coelhos e galinhas num total de 20 cabeças e 58 pés. Determine o número de coelhos e de galinhas.

Coelhos: x 

Galinhas: y

Isolando y na equação (1):

Substituindo (3) em (2):

Substituindo x = 9 em (3):

Resposta: Este senhor tem 9 coelhos e 11 galinhas.

5 - Num estacionamento há 14 veículo entre carros e motos, total de 48 rodas. Quantos carros e quantas motos há nesse estacionamento?

Resolução:

Motos: x

Carros: y

Veículos: x + y = 14

Números de rodas: 2x + 4y = 48

Vamos resolver esse sistema pelo método da substituição:

Isolando x em (1):

x = 14 – y  (3)

Substituindo o valor de x em (2):

Substituindo o valor de y em (3):

Resposta: Há nesse estacionamento 10 carros e 4 motos. 

Problemas com porcentagens

1 - Quanto é 32 % de R$ 25 000,00?
Resolução:

Resposta: R$ 8 000,00

 2 - Em um grupo de 20 pessoas, 40% são homens e 75% das mulheres são solteiras. O número de mulheres casadas é:

a) 3                 b) 6                c) 7              d) 8

Resolução:

Números de homens:

= 8 homens

Números de mulheres:

20 – 8 = 12 mulheres

Números de mulheres casadas:

100% – 75% = 25%

Resposta: 3 mulheres casadas.

3 - Quanto é 25% da terça parte de 1026?

a) 855

b) 769,5

c) 94,5

d) 85,5

Resolução:

Área e perímetro dos quadriláteros

1 - Um terreno retangular tem 128 metros de perímetro. O comprimento tem 20 metros a mais que a largura. Qual é a área desse terreno?
a) 440 m²
b) 924 m²
c) 960 m²
d) 640 m²

Resolução:

O perímetro é a soma dos lados:
x + x + 20 + x + 20 = 128
4x + 40 = 128
4x = 128 – 40
4x = 88

x = 22

Cálculo da área:

b = x + 20 = 22 + 20 = 42

h = x = 22

A = b⋅h

A = 42 m⋅22 m

A = 924 m²         

2 - Calcule o perímetro do trapézio retângulo da figura:                                                                   
Resolução:

Primeiramente vamos calcular a altura desse trapézio.

h = ?
B = 33 m
b = 15 m
A = 576 m²

h = 24 m

Agora vamos calcular a quarta medida do lado do trapézio, usando o teorema de Pitágoras, no triângulo retângulo:

x = 30 m

Perímetro do trapézio:

P = 15 m + 24 m + 33 m + 30 m

P = 102 m

3 - Qual é a área do trapézio retângulo da figura?

a) 42 m²
b) 92 m²
c) 96 m²
d) 64 m²

Resolução:

Primeiramente teremos de calcular a altura desse trapézio.   

Usando o teorema de Pitágoras para calcular a altura (h) no triângulo retângulo:

10² = h² + 8²

10⋅10 = h² + 8⋅8

100 = h² + 64

100 – 64 = h²

36 = h²

h = 6 m

Para calcular a área do trapézio, vamos usar a fórmula:

A = ?

b = 12 m

B = 20 m

4 - (OBMEP 2019) O quadrado abaixo está dividido em dois triângulos e um quadrilátero. O triângulo 1 tem o dobro da área do triângulo 2. Qual é a área do quadrilátero 3?

a) 36 cm²

b) 48 cm²

c) 52 cm²

d) 56 cm²

Área do triângulo 1:

Área do triângulo 2:

Área do quadrado:

Área do quadrilátero 3: