Frações Equivalentes

Frações equivalentes são frações que, apesar de terem numeradores e denominadores diferentes, representam a mesma quantidade ou proporção. Por exemplo, as frações $\frac{1}{2}\backslash frac\{1\}\{2\}$ e $\frac{2}{4}\backslash frac\{2\}\{4\}$ são equivalentes porque ambas representam a metade de um todo. Conceito Básico Duas frações $\frac{a}{b}\backslash frac\{a\}\{b\}$ e $\frac{c}{d}\backslash frac\{c\}\{d\}$ são equivalentes se, ao multiplicar cruzado, obtivermos a mesma quantidade: a×d=b×c $$$$ Isso significa que, independentemente dos valores dos numeradores e denominadores, a relação entre os valores é a mesma. Como Encontrar Frações Equivalentes Multiplicação: Para encontrar uma fração equivalente, você pode multiplicar o numerador e o denominador da fração por um mesmo número. Exemplo: Multiplicar $\frac{3}{5}\backslash frac\{3\}\{5\}$ por 2. $$\frac{3\times 2}{5\times 2}=\frac{6}{10}$$ Aqui, $\frac{8}{12}\backslash frac\{8\}\{12\}$ e $\frac{2}{3}\backslash frac\{2\}\{3\}$ são frações equivalentes: 8×3 = 12×2 = 24 Exemplo de Verificação Para verificar se $\frac{4}{6}\backslash frac\{4\}\{6\}$ e $\frac{2}{3}\backslash frac\{2\}\{3\}$ são equivalentes, basta multiplicar cruzado: $$4\times 3=12\mathrm{<br>}4\; \backslash times\; 3\; =\; 12$$ $$6\times 2=126\; \backslash times\; 2\; =\; 12$$ Como ambos os produtos são iguais, as frações $\frac{4}{6}\backslash frac\{4\}\{6\}$ e $\frac{2}{3}\backslash frac\{2\}\{3\}$ são equivalentes. Fração irredutível  Uma fração irredutível é uma fração que não pode ser simplificada, ou seja, o numerador e o denominador não podem ser divididos pelo mesmo número: Para obter uma fração irredutível, é necessário dividir os termos pelo máximo divisor comum entre o numerador e o denominador.  Quando uma fração é irredutível, dizemos que o numerador e o denominador são primos entre si. Exemplos de frações irredutíveis são 3/4, 4/5 e 3/7.  Exemplos de frações redutíveis são 9/12 e 12/18, pois o numerador e denominador podem ser divididos por 3 e 12, respectivamente.  Exercícios 1 - Qual das frações abaixo é equivalente a 2/5? Resolução: 2 - Dada a fração abaixo, qual das alternativas é igual a, respectivamente, uma fração equivalente a ela e à sua fração irredutível? 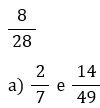Resolução: Resposta: Letra B