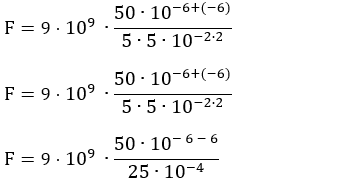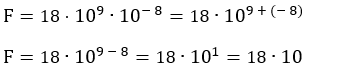Essa força é descrita pela Lei de Coulomb, que afirma que a intensidade da força entre duas cargas é diretamente proporcional ao produto das cargas e inversamente proporcional ao quadrado da distância entre elas. A expressão matemática é:
Onde:
Quando estamos trabalhando com o vácuo utilizamos ε0 (permissividade elétrica no vácuo), nesse caso, ε0 vale 8,85 x 10-12C2/N⋅m2, e portanto, utilizando a equação descrita anteriormente k0 vale 9 x 109 N⋅m2/C2. Relação entre força elétrica e campo elétricoO Campo Elétrico (E) é definido como a força elétrica por unidade de carga. Em termos matemáticos, é expresso como E = F/q, onde F é a força sobre uma carga de teste q.A força elétrica pode ser atrativa (quando as cargas têm sinais opostos) ou repulsiva (quando as cargas têm o mesmo sinal). Essa interação é fundamental para explicar fenômenos como a formação de átomos, moléculas e os comportamentos de materiais em diferentes contextos: EXEMPLOS 1 - (Unifesp) Duas partículas de
cargas elétricas Q = 4,0⋅10−16 C e q = 6,0⋅10−16 C estão separadas no vácuo por
uma distância de 3,0⋅10−9 m.
Sendo ko = 9 ⋅109 N⋅m2 / C2, a intensidade da força de interação entre elas,
em newtons, é de: A) 1,2⋅10−5 N B) 1,8⋅10−4 N C) 2,0⋅10−4 N D) 2,4⋅10−4 N E) 3,0⋅10−3 N Resolução: Q = 4,0⋅10−16 C q = 6,0⋅10−16 C
k0 = 9⋅109 N⋅m2 / C2    F = 2,4⋅10−4 N 2 - (Mack-SP) Uma carga elétrica puntiforme com q = 4,0 μC, que é colocada em um ponto P do vácuo, fica sujeita a uma força elétrica de intensidade 1,2 N. O campo elétrico nesse ponto P tem intensidade: a) 3,0∙105 N/C b) 2,4∙105 N/C c) 1,2∙105 N/C d) 4,0∙10−6 N/C e) 4,8∙10−6 N/C Resolução: E = ? F = 1,2 N q = 4,0 μC = 4,0⋅10 – 6 C 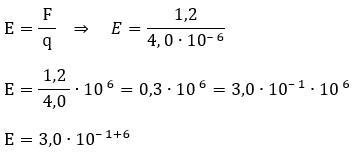 E = 3,0∙105 N/C EXERCÍCIOS 1 - Duas cargas puntiformes de valores Q1 = 5μC e Q2
= − 10μC estão a uma distância de 5 cm. Qual é a força elétrica entre
elas? Determine também se ela é repulsiva ou atrativa.
A) 180 N, atrativa. B) 100 N, repulsiva. C) 180 N, repulsiva. D) 1000 N, atrativa. E) 1,8 N, atrativa. Resolução: Q1 = 5μC = 5⋅10 – 6 C Q2 = − 10μC = − 10⋅10 – 6 C k = 9⋅109
N⋅m2 / C2 r = 5 cm = 5:100 m = 0,05 m = 5⋅10 –
2 m F = ?  A força elétrica é atrativa, porque as cargas possuem sinais
contrários. 2 - Uma carga elétrica com valor de 10 μC possui
campo elétrico com valor de 3,0∙105 N/C. Determine a força
elétrica gerada. A) 3,0 N B) 10∙103 N C) 3,0∙10−2 N D) 3,0∙10−3 N
E) 3,0∙102 N Resolução: E = 3,0∙105 N/C q = 10⋅10 – 6 C F = ?
  F = 3 N 3 - Uma partícula possui campo elétrico com valor
de 200∙105 N/C e força elétrica com valor de 5,0∙105 N.
Determine o valor da carga elétrica. A) 0,025 C B) 0,05 C C) 0,055 C D) 0,045 C E) 0,035 C Resolução: E = 200∙105 N/C
F = 5,0∙105 N q = ?  q = 0,025 C 4 - Uma carga q e outra Q,
com o dobro de q, estavam inicialmente a uma distância d e
foram reposicionadas a uma distância equivalente ao dobro da inicial. A força
elétrica final será de quanto da força inicial?  Resolução: Força inicial:  Força final:  Multiplicando o numerador e o denominador da fração por 2:   Logo: A) 0,9 B) 0,6 C) 0,5 D) 0,3 E) 0,1 Resolução: q1 = q2 = 2⋅10 – 6 C F = 0,1N k = 9⋅109
N⋅m2 / C2 r = ?    r = 0,6 m |