Relações métricas no triângulo retângulo

No triângulo retângulo ABC da figura, temos:

“a” é a hipotenusa,

“b” e ”c” são os catetos,

“m” é a projeção do cateto “b” sobre a hipotenusa,

“n” é a projeção do cateto “c” sobre a hipotenusa. 

Relações métricas:

Lembrando que: a = m + n  e que a² = b² + c² é o teorema de Pitágoras.

Exercícios:

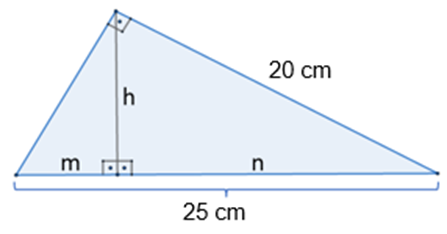
1– Determine as medidas de “a” e “m” indicadas no triângulo retângulo a seguir.

Resolução:

Como a = 25 e c = 20, teremos:

2 – Determine as medidas de “a” e “m” indicadas no triângulo retângulo a seguir.

Resolução:

Como h = 15 e n = 9, teremos:

3 – Determine as medidas de "m" e "n" indicadas no triângulo retângulo a seguir.

Resolução:

Como a = 16 e b = 8:

4 – Determine as medidas dos elementos desconhecidos, no seguinte triângulo retângulo.

Resolução:

Como m = 21 e n = 4:

   

   

5 – Em um retângulo, a medida da diagonal é expressa por (x + 8) cm e as medidas dos lados são expressas por x cm e 12 cm. Nessas condições, qual é o perímetro desse retângulo?

Resolução:

Aplicando o teorema de Pitágoras:

 

 

Como perímetro do retângulo(soma dos lados), teremos:

    P = x + 12 + x + 12

    P = 5 + 12 + 5 + 12
    P = 34 cm

Sistema de equações do 1° grau com duas incógnitas: Método de tentativa e erro

Para resolver sistemas de equações do 1° grau com duas incógnitas, podemos usar vários métodos de resolução o método de tentativa e erro é aplicado em sistemas simples de equações, em que possamos realizar mentalmente. Esse método consiste em encontrar um par de  números que substituindo em cada equação, torne a sentença verdadeira.

1 - Vamos resolver o sistema de equações abaixo por tentativas:

Resolução:

Logo, x = 4 e y = 3                  Solução: (4, 3)

2 - Resolver o sistema de equações abaixo por tentativa e erro:

Resolução:

Logo, x = 15 e y = 5                  Solução: (15, 5)

3 - Resolver o sistema de equações abaixo por tentativas:

Resolução:

Logo, x = 25 e y = 17            Solução: (25, 17)

4 - Resolver o sistema de equações do 1° grau com duas incógnitas:

Resolução:

Logo, x = 10 e y = 4

Solução: (10, 4)

Soma dos termos de uma progressão aritmética (P.A.)

1 - Dada a progressão aritmética (4, 8, 12, 16, …), calcule a soma dos seus 110 primeiros termos.

Resolução:

Primeiramente vamos calcular o valor do 110° termo:

Cálculo da soma dos seus 110 primeiros termos:

2 - Calcule a soma dos 50 primeiros termos da progressão aritmética (4, 8, 12, 16, …)

Resolução:

Primeiramente vamos calcular o termo a₅₀ dessa progressão aritmética: 

Fazendo n = 50 na fórmula da soma:

Substituindo os valores de a₁ e a₅₀:

3 - Na seguinte sequência (-7,-1,5,11...) é uma P.A de uma certa razão, pergunta se qual é a soma dos 15 primeiros desta sequência?

Resolução:

Primeiramente vamos calcular o valor do 15° termo:

Cálculo da soma dos seus 15 primeiros termos:

4 - Qual é a soma de todos os números de dois algarismos que têm resto 2 quando dividido por 3?

a) 3270

b) 2645

c) 2160

d) 1635

Resolução:

Vamos encontrar os primeiros menores números de dois algarismos que têm resto 2 quando divididos por 3:

Vamos encontrar os últimos maiores números, com dois algarismos que têm resto 2 quando divididos por 3:

Esses números formam uma progressão aritmética (P. A.) de razão 3: 

11, 14, 17, ..., 98.

5 - Joana comprou um celular e dividiu o pagamento em 24 parcelas mensais que formam uma progressão aritmética crescente. As três primeiras parcelas foram de R$ 120,00, R$ 126,00 e R$ 132,00. Sabendo que, ao final, constatou-se que Joana não pagou a 19ª parcela, o valor pago por ela foi:

a) R$ 3.954,00
b) R$ 4.026,00
c) R$ 4.200,00
d) R$ 4.308,00
e) R$ 4.382,00

Resolução:

Primeiramente vamos calcular o termo a₂₄ e a₁₉ dessa progressão aritmética:

Fazendo n = 24 na fórmula da soma:

Substituindo os valores de a₁ e a₂₄:

Valor pago:

Retas paralelas cortadas por uma transversal

Exercícios

1 – As retas “r” e “s” na figura são concorrentes, os ângulos “m” e “n” a seguir são:

a. (    )  colaterais internos.

b. (    )  alternos externos.

c. (    )  correspondentes.                        

d. (    )  opostos pelo vértices.

2 – Sendo r //s, os ângulos “e” e “f” na figura seguinte são:

a. (    )  colaterais externos.

b. (    )  alternos externos.

c. (    )  correspondentes.                        

d. (    )  alternos internos.

3 – Sendo r //s, os ângulos “m” e “n” na figura seguinte são:   

        

a. (    )  colaterais internos.

b. (    )  alternos internos.

c. (    )  alternos externos.

d. (    )  correspondentes.  

 

4 – Sendo r //s, os ângulos “b” e “g” na figura seguinte são:

a. (    )  colaterais internos.

b. (    )  correspondentes

b. (    )  alternos externos.                         

c. (    )  alternos internos.

5 – Sendo r //s, os ângulos “b” e “f” na figura seguinte são:

a. (    )  colaterais internos.

b. (    )  alternos externos.

c. (    )  correspondentes.                        

d. (    )  opostos pelo vértices.

Respostas:

1 – Os ângulos “m” e “n” são opostos pelo vértices.

2 – Os ângulos “e” e “f” são colaterais externos.

3 – Os ângulos “m” e “n” são alternos internos.

4 –  Os ângulos “b” e “g” são alternos externos. 

5 – Os ângulos “b” e “f” são correspondentes.  

6 – Se r//s, determine os valores dos ângulos indicados pelas letras x e y.

Resolução:

  Ângulos correspondentes

 Ângulos opostos pelo vértice

Logo, y = 40°

7 – As retas "r" e "s"  na figura abaixo são paralelas. Determine a medida de x

Resolução:

8 – As retas r e s da figura são paralelas cortadas por uma transversal t. Determine o valor de x.

Resolução:

Ângulos colaterais externos são suplementares (soma 180°):

3x + x + 20° = 180°

4x + 20° = 180°

4x = 180° – 20°

4x = 160°

x = 160°/4

x = 40°