Potências são o resultado de produtos em que todos os fatores são iguais. Por isso elas são representadas de maneira simplificada por meio de uma base, que é o número multiplicado, e de um expoente, que é a quantidade de vezes que esse número é multiplicado.
Como os números das multiplicações são todos iguais, podemos escrever cada expressão de forma abreviada:
Quando o expoente de uma potência é negativo, precisamos usar algumas das propriedades de potência para conseguir calculá-la. Uma dessas propriedades é a potência de frações, e a outra é a própria potência com expoente negativo.
Quando uma potência possui expoente negativo, a propriedade usada para calculá-la é a seguinte:
Para resolver potências cujo expoente é negativo, fazemos da seguinte maneira:
Escreva a base da potência na forma de fração;
Inverta a base e também o sinal do expoente;
Faça os cálculos e, se necessário, com as propriedades de potência.
Se a base da potência for uma fração podemos escrever:

Exemplos:
Exercícios
1 - Calcule a potência de expoente negativo a seguir:
Resolução:
2 - Qual dos resultados a seguir é solução da potência
a) 0,01
b) 0,001
c) 0,0001
d) 0,00001
Resolução:
3 - Calculando o valor da potência
Vamos ter:
a) 2
b) 0,5
c) -2
d) – 0,5
Resolução:
4 - Calculando o valor da potência de expoente negativo a seguir:
Resolução:
5 - Calcule o valor de cada potência:












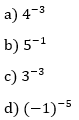

Nenhum comentário:
Postar um comentário