O Teorema de Pascal, ou Princípio de Pascal, é um dos fundamentos da hidrostática e estabelece que a pressão exercida em um fluido incompressível se transmite integralmente e uniformemente em todas as direções dentro do fluido e para as paredes do recipiente que o contém.
O teorema de Pascal pode ser calculado por meio da sua fórmula:


A1 e 𝐴2 → áreas relacionadas à aplicação das forças, medidas em [m2]
H1 e H2 → alturas relacionadas às áreas, medidas em metros [m]
Conceitos Importantes:
- Transmissão
da Pressão: Qualquer variação de pressão aplicada a um fluido
confinado é transmitida sem perda para todas as partes do fluido.
- Aplicações:
Esse teorema é essencial no funcionamento de sistemas hidráulicos, como
prensas hidráulicas, freios de automóveis e macacos hidráulicos.
- Fluidos
Incompressíveis: O princípio se aplica a líquidos, pois eles não podem
ser comprimidos facilmente, garantindo que a pressão seja distribuída de
maneira uniforme.
1 – Uma prensa hidráulica tem pistões com áreas de 10 cm2
e 100 cm2. Se uma força de 10 N é aplicada no pistão menor, qual a
força no pistão maior?
Resolução:
A pressão no pistão menor é transmitida para o pistão maior:
F2 = ?
A1 = 10 cm2
A2 = 100 cm2

2 - (Espcex) Um elevador hidráulico de um posto de gasolina é acionado por um pequeno êmbolo de área igual a 4 x 10 – 4 m2. O automóvel a ser elevado tem peso de 2 x 10 4 N e está sobre o êmbolo maior, de área 0,16 m2. A intensidade mínima da força que deve ser aplicada ao êmbolo menor para conseguir elevar o automóvel é de:
a) 20 N b) 40 N c) 50 N d) 80 N e) 120 N
Resolução:
p2 = p2
F1 = ?
p1 = p2
F2 = P2 = 2 x 10 4 N
A1 = 4 x 10 – 4 m2
A2 = 0,16 m2
0,16 ⋅ F1 = 4 x 10 – 4 ⋅ 2 x 10 4
0,16 F1 = 8 x 10 – 4 + 4 ⇒ 0,16 F1 = 8 x 10 0
a) 30 N
b) 60 N
c) 480 N
d) 240 N
e) 120 N
Resolução:
F2 = ?
F1 = 120 N
D1 = 10 cm
Como o diâmetro é o dobro do raio:
d = 2r


Aplicando o
Princípio de Pascal:
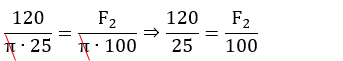

F2 = 480 N
Exercícios
1 - (FPS-PE) A figura abaixo mostra o princípio de
funcionamento de um elevador hidráulico, formado por um sistema de vasos
comunicantes contendo um fluído incompressível no seu interior. Considere que a
aceleração da gravidade vale 10 m/s2. Sabendo-se que as áreas das
seções transversais dos pistões 1 e 2 são, respectivamente, A1 =
0,2 m2 e A2 = 1 m2, o módulo da
força F1 necessária para erguer o peso equivalente de uma carga
com massa igual a 100 kg será:

a) 10 N
b) 50 N
c) 100 N
d) 150 N
e) 200 N
Resolução:
O peso da carga colocada sobre a área maior corresponde a
1000 N e equivale à força F2, aplicada sobre o êmbolo maior.
F2 = P
m = 100 kg e g = 10 m/s2
A1 = 0,2 m2 e A2 = 1 m2
A força F1 será determinada a partir da
aplicação do Princípio de Pascal.

F1 = 0,2⋅1000 ⇒ F1 = 200 N
2 - (UNICAMP) A figura abaixo mostra, de forma simplificada, o sistema de freios a disco de um automóvel. Ao se pressionar o pedal do freio, este empurra o êmbolo de um primeiro pistão que, por sua vez, através do óleo do circuito hidráulico, empurra um segundo pistão. O segundo pistão pressiona uma pastilha de freio contra um disco metálico preso à roda, fazendo com que ela diminua sua velocidade angular.
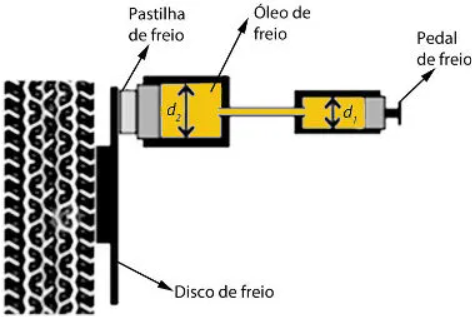
Considerando o diâmetro d2 do
segundo pistão duas vezes maior que o diâmetro d1 do
primeiro, qual a razão entre a força aplicada ao pedal de freio pelo pé do
motorista e a força aplicada à pastilha de freio?
a) 1/4.
b) 1/2.
c) 2.
d) 4.
Resolução:
Para aplicar o Princípio de Pascal, temos que:
F1 = Força aplicada ao pedal pelo pé do
motorista;
R1 = Raio do pistão do freio;
d1 = Diâmetro do pistão do freio;
F2 = Força aplicada sobre o disco de freio;
R2 = Raio do pistão do disco de freio;
d1 = Diâmetro do pistão do disco de freio;
Se d2 é o dobro de d1 podemos
afirmar que R2 é o dobro de R1. Sabendo que a área
de um sistema circular é dada por π⋅R2,
podemos escrever que:

Simplificando:
Como:


Multiplicando cruzado:
As secções retas dos pistões são indicadas por S1 e
S2, tendo-se S2 = 4S1.
A força exercida sobre o fluido tem intensidade F1 e
a força exercida pelo fluido tem intensidade F2. A situação descrita
obedece:
a) ao Princípio de Arquimedes e, pelas leis de Newton, conclui-se
que F1 = F2 = P;
b) ao Princípio de Pascal e, pelas leis de ação e reação e de
conservação da emergia mecânica, conclui-se que F2 = 4F1 =
P;
c) ao Princípio de Pascal e, pela lei da conservação da energia,
conclui-se que F2 = 4F1 ≠ P;
d) apenas às leis de Newton e F1 = F2 = P;
e) apenas à lei de conservação de energia.
Resolução:

Como: S2 = 4S1

Multiplicando cruzado:
Como o sistema está em equilíbrio:
Resposta: Letra B
4 - (UERJ-RJ) Um adestrador quer saber o peso de um elefante.

Resolução:
F1 = F = 200 N
A1 = 25 cm2 A2 = 2 000 m2
O peso do elefante será determinado a partir da
aplicação do Princípio de Pascal:
25⋅P = 200⋅2 000 ⇒ 25P =
400 000
5 - (UFJF-MG) Um grupo de alunos resolveu montar um guindaste hidráulico para uma feira de ciências (veja figura).

Para isso resolveram utilizar duas seringas. Uma seringa tem
diâmetro D1 = 2 cm e a outra D2 = 1 cm. Sabendo que o
módulo da força máxima que o motor permite produzir é de 2 N, qual o valor
máximo da massa M que o guindaste poderá erguer? (g = 10 m/s2).
a) 600 g. b)
800 g. c) 1 000 g. d) 1 200 g. e) 200
g.
Resolução:
D1 = 2 cm = 2:100 m = 0,02 m
D2 = 1 cm = 1:100 m = 0,01 m
Como o diâmetro é o dobro do raio:
D = 2R




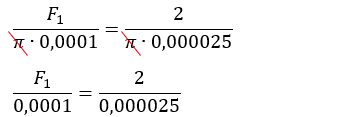
Multiplicando cruzado:


Simplificando:

P = m ⋅ g
8 = m ⋅ 10
6 - (FGV-SP) O macaco hidráulico consta de dois êmbolos: um
estreito, que comprime o óleo, e outro largo, que suspende a carga. Um sistema
de válvulas permite que uma nova quantidade de óleo entre no mecanismo sem que
haja retorno do óleo já comprimido. Para multiplicar a força empregada, uma
alavanca é conectada ao corpo do macaco.

Tendo perdido a alavanca do macaco, um caminhoneiro de massa 80 kg,
usando seu peso para pressionar o êmbolo pequeno com o pé, considerando que o
sistema de válvulas não interfira significativamente sobre a pressurização do
óleo, poderá suspender uma carga máxima, em kg, de
Dados: diâmetro do êmbolo menor = 1,0 cm; diâmetro do êmbolo maior
= 6,0 cm; aceleração da gravidade = 10 m/s2
a) 2 880. b) 2 960. c) 2 990. d) 3 320. e) 3 510.
Peso do caminhoneiro:
m = 80 kg g = 10 m/s2
P1 = m1 ⋅ g
P = 80 ⋅ 10 ⇒ P = 800 N
D1 = 1 cm = 1:100 m = 0,01 m
D2 = 6 cm = 6:100 m = 0,06 m
Como o diâmetro é o dobro do raio:
D = 2R
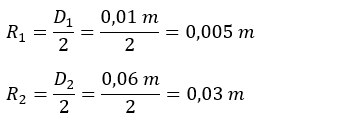

P = F1 = 800 N


Multiplicando cruzado:

F2 = 32 ⋅ 900
F2 = 28 800 N
F2 = P2 = m2 ⋅ g
28 800 = m2 ⋅10
m2 = 2 880 kg
7 - (CEFET-RS) A figura representa um elevador hidráulico de
um posto de lavagem de automóveis.

a) Qual deve ser a pressão exercida pelo cilindro (acima da
atmosférica) para equilibrar o automóvel (iminência de iniciar a subida)?
b) Qual será o deslocamento do cilindro para elevar o automóvel de
20cm?
Resolução:
a) A pressão
exercida pelo cilindro é a mesma que a exercida pelo êmbolo:
P = m⋅g ⇒ P = 3⋅103 ⋅10
P = 30⋅103 N
P = F2
A2 = 6⋅10-3 m2

p = 5⋅103+3
p = 5⋅106 N/m2
H2 = 20 cm = 20 : 100 m = 0,2 m
A1 = 3⋅10-5 m2 A2 = 6⋅10-3 m2



H1 = 40 m
8 - (CFT-MG) O esquema seguinte ilustra o funcionamento de uma espingarda de ar comprimido.

Admitindo que perdas de pressão e o atrito entre o chumbinho e o cano sejam desprezíveis, a velocidade do projétil, em m/s, imediatamente após ser expelido dessa arma, e igual a
a) 100. b) 200. c) 300. d) 400.
Resolução:
m = 1 g = 1:1 000kg = 0,001 kg
A1 = 10 πcm2
A2 = 0,05 πcm2
F1 = 4 000N
△s = 1 m
vo = 0
v = ?

Multiplicando cruzado:
1⋅F2 = 400⋅0,05 ⇒ F2 = 20 N
Usando o teorema Trabalho - Energia (Trabalho = Variação da energia cinética):

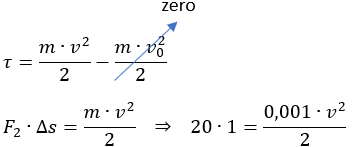



a) 100
N
b) 300
N
c) 600 N
d) 900
N
e) 1 000 N
Resolução:
m = 9 000 kg g = 10 m/s2
P = m⋅g
P = 90 000 N
FP = P = 90 000 N
Como o diâmetro é o dobro do raio:
d = 2r


FF = 100 N
10 - (UFRN-RN) Do ponto de vista da Física, o sistema de freios dos carros atuais é formado por uma alavanca e por uma prensa hidráulica. Enquanto a alavanca tem a capacidade de ampliação da força aplicada por um fator igual à razão direta de seus braços, a prensa hidráulica amplia a força da alavanca na razão direta de suas áreas. Finalmente, a força resultante aciona os freios, conforme mostrado na Figura, fazendo o veículo parar.



Simplificando:
𝐹3 = 32⋅𝐹1
Resposta: Letra A.
11 - (UNESP-SP) As áreas dos pistões do dispositivo hidráulico da figura mantêm a relação 50:2. Verifica-se que um peso P, quando colocado sobre o pistão maior, é equilibrado por uma força de 30N no pistão menor, sem que o nível do fluido nas duas se altere.


12 - (UFSC-SC) – O trecho do livro “Jorge, um
brasileiro”, apresentado na questão discursiva 3, menciona que o fluido de
freio tinha acabado, ficando subtendido que, para o freio do carro funcionar, é
necessário colocar fluido no sistema de freios. O fluido de freio é parte vital
para o funcionamento do mesmo, pois ele é responsável por transmitir a força
(F₁) aplicada ao pedal do freio para o pistão 2.
A seguir, apresentamos, de maneira simples e
esquemática, o sistema de freio de um carro. Ele é constituído de um pedal, que
empurra o pistão 1 e, consequentemente, desloca o fluido de freio e empurra o
pistão 2 e a pastilha de freio contra o disco de freio. Desta maneira, o
motorista consegue parar o carro.

d₁ = 0,4 m
d₂ = 0,2 m
Área do pistão 1 = 4⋅10⁻⁴
m²
Área do pistão 2 = 16⋅10⁻⁴
m²
a) Qual o tipo de alavanca que o pedal de freio
representa, na forma como é aqui apresentado?
b) Enuncie o Princípio de Pascal.
c) Com base em princípios de física e explicitando o raciocínio matemático, determine a força que o pistão 2 exerce sobre a pastilha de freio, supondo que o motorista empurrou o pedal até o fundo e para isto aplicou uma força (F₁) de intensidade 100 N.
Resolução:
a) A alavanca
é o tipo inter-resistente, pois a força potente e o ponto de apoio estão nas
extremidades e a força resistente está no meio, entre elas.
b) O
Princípio de Pascal enuncia que a pressão aplicada a um fluido confinado
transmite-se, em todo o seu interior, sem diminuição, em todas as direções.
c) Na alavanca:
𝐹1⋅0,4 =
Como F1=100N:
Nos pistões:
Simplificando:

13 - (FATEC-SP) Um esquema simplificado de uma
prensa hidráulica está mostrado na figura a seguir. Pode-se fazer uso de uma
alavanca para transmitir uma força aplicada à sua extremidade, amplificando seu
efeito várias vezes.

Supondo que se aplique uma força de 10 N à
extremidade A da alavanca e sabendo que a razão entre a área do êmbolo maior
pela área do êmbolo menor é de 5, o módulo da força F que o êmbolo maior
aplicará sobre a carga será de:
a) 4 N
b) 20 N
c) 50 N
d) 100 N
e) 200 N
Resolução:
F = 10 N
d = 20 cm
d1 = 10 cm
a2 = 5⋅ a1
Na alavanca:
F⋅d = 𝐹1⋅
d1 ⟶ 10⋅20 = 𝐹1⋅10
𝐹1 = 20 N
Nos pistões, usando o teorema de Pascal:
𝐹2 = 2 0⋅5 ⇒ 𝐹2 = 100 N
Resposta: Letra D
14 – (UFPE-PE) Uma força vertical de intensidade F, atuando sobre o êmbolo menor de uma prensa hidráulica, mantém elevado um peso P = 400 N, como mostra a figura.
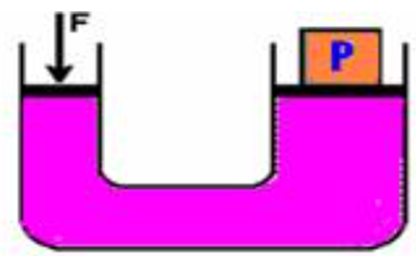
Sabendo que a área do êmbolo maior é 8 vezes a área menor,
determine o valor de F, em newtons.
Resolução:
F = ?
F2 = P
= 400 N
A2 = 8⋅A1
Fazendo F1 = F e usando o teorema de Pascal:
Simplificando:

F = 50 N
15 - (FUVEST-SP) Considere o arranjo da figura,
onde um líquido está confinado na região delimitada pelos êmbolos A e B, de
áreas a = 80 cm2 e b = 20 cm2, respectivamente. O
sistema está em equilíbrio. Despreze os pesos dos êmbolos e os atritos. Se mA
= 4,0 kg, qual o valor de mB?

a) 4 kg b) 16 kg c) 1 kg d) 8 kg e) 2 kg
Resolução:
a = 80 cm2, b = 20 cm2 e mA
= 4,0 kg
mB = ?
PA = mA⋅g = 4⋅g
PB = mB⋅g
Usando o teorema de Pascal:
8⋅mB = 4⋅2
⇒ 8⋅mB =
8
mB = 1 kg
Resposta: Letra C
16 - (UFRS-RS) A
figura mostra três tubos cilíndricos interligados entre si e contendo um
líquido em equilíbrio estático. Cada tubo possui um êmbolo, sendo a área da
secção reta do tubo 1 a metade da área da secção reta do tubo 2 e da do tubo 3;
os êmbolos se encontram todos no mesmo nível (conforme a figura a seguir).O
líquido faz uma força de 200N no êmbolo 1.

As forças que os êmbolos 2 e 3, respectivamente,
fazem no líquido valem
a) 200 N e 200 N.
b) 400 N e 400 N.
c) 100 N e 100 N.
d) 800 N e 800 N.
e) 800 N e 400 N.
Resolução:
A2 = A3

a) 100 N b) 200 N c) 300 N d) 400 N e) 500 N
Resolução:
F⋅d = F1⋅ d1 ⇒ 50⋅200 = F1⋅ 40
10 000 = 𝐹1⋅40
F1 = 250 N

F2 = 250⋅2 ⇒ F2 = 500 N
Resposta: Letra E
18 - (UNIDERP-MS) A figura mostra o funcionamento de uma
prensa hidráulica para comprimir um fardo.

a) A1 – A2 b) A2
– A1 c) A1⋅ A2 d) A1 / A2 e)
A2/A1
Resolução:
Sendo a pressão em cada êmbolo a mesma:

Multiplicando cruzado:
19 - (UFRGS) Assinale a alternativa que
preenche corretamente as lacunas do texto que segue, na ordem em que aparecem.
A figura a seguir representa uma prensa hidráulica
composta por dois pistões, de diâmetros d1 e d2. O
motor aplica uma força axial de intensidade F1 = 100 N no
pistão de diâmetro d1= 0,05 m. Para que se possa obter uma força de
intensidade F2 = 10 000 N no pistão de diâmetro d2,
esse diâmetro deve ser igual a ___________, e a pressão transmitida será de
____________.

a) 0,25 m; 50,9
kPa
b) 0,50 m; 12,7
kPa
c) 0,50 m; 50,9 kPa
d) 0,12 m; 50,9 kPa
e) 0,12 m; 12,7 Pa
Resolução:
d2 = ?
p = ?
F1 = 100 N
F2 = 10 000 N
d1= 0,05 m
Como o diâmetro é o dobro do raio:
d = 2r




Multiplicando
cruzado:


r2
= 0,25 m
Como d = 2r:
d2 =2⋅r2
d2 =2⋅0,25 m ⇒ d2 = 0,5 m
Como a pressão é igual em todos os pistões:
F1 = 100 N π ≅ 3,1416


Resposta: Letra C
20 - (UNB-DF) Temos dois tubos cilíndricos A e B
de diâmetro D e D/4, respectivamente.

Os cilindros formam um sistema de macaco hidráulico e os êmbolos são móveis. Considerando o sistema em equilíbrio e desprezando o peso dos êmbolos, ache a razão entre as intensidades das forças FA/FB.
Resolução:
DA = D
Como o diâmetro é o dobro do raio:
d = 2r



Aplicando o
Princípio de Pascal:

Multiplicando cruzado:

21 - (CPS-SP) No início do século XX, a indústria e o comércio da cidade de São Paulo possibilitaram uma qualidade de vida melhor para seus habitantes. Um dos hábitos saudáveis, ligados à higienização bucal, foi a utilização de tubos de pasta dental e as respectivas escovas de dente.

Considerando um tubo contendo pasta dental de densidade homogênea, uma pessoa resolve apertá-lo. A pressão exercida sobre a pasta, dentro do tubo, será:
a) maior no fundo do tubo, se apertar no fundo.
b) menor no fundo do tubo, se apertar perto do bico de saída.
c) maior no meio do tubo, se apertar no meio.
d) menor no fundo do tubo, se apertar no meio.
e) igual em todos os pontos, qualquer que seja o local apertado.
- Princípio de Pascal:
A pressão em um fluido incompressível se transmite igualmente em todas as direções.
- Fluido incompressível:
A pasta de dente é considerada um fluido incompressível, o que significa que sua densidade não muda significativamente com a pressão.
- Efeito na pasta:
Quando se aperta um tubo de pasta de dente, a pressão é aplicada em um ponto específico, mas essa pressão se espalha e se distribui igualmente em toda a pasta, independentemente de onde seja apertada.
Resposta: Portanto, a correta é a (e) igual em todos os pontos, qualquer que seja o local apertado.
22 - (CFT-MG) O sistema de freio hidráulico de um veículo está baseado no princípio

b) de Arquimedes.
c) da ação e reação.
d) da inércia.
Resolução:
O sistema de freio hidráulico utiliza um fluido (geralmente óleo
de freio) para transmitir a força de frenagem do pedal para as
rodas. Quando o motorista aciona o pedal, a pressão do fluido é
transmitida aos cilindros de freio nas rodas, que então pressionam as pastilhas
contra os discos, gerando a frenagem. Este processo é possível devido à
Lei de Pascal, que afirma que a pressão é transmitida uniformemente pelo fluido.
23 - (UFSM-RS) Um braço mecânico de um trator usado para fazer valetas tem um sistema hidráulico que se compõe, basicamente, de dois cilindros conectados por uma mangueira resistente a altas pressões, todos preenchidos com óleo.

Se, no equilíbrio, P é a pressão num cilindro, a pressão no outro,
que tem área 10 vezes maior, é
a) 10P b) 5P c) P d) 5/P e) P/10
Resolução:
O princípio de Pascal afirma que a pressão em ambos os
cilindros é a mesma.
P1 = P2
A pressão no primeiro cilindro é P.
P1 = P
Portanto, a pressão no segundo cilindro também é P.
P2 = P
Portanto, a pressão no segundo cilindro também é P.
24 - (CFT-SP) A figura a seguir mostra, de maneira esquemática, como funciona o freio de um automóvel. Ao pressionar o pedal 1 empurramos o óleo que se encontra no cilindro 2, que passa para o cilindro 3 onde aciona o freio 4, agindo sobre a roda 5.
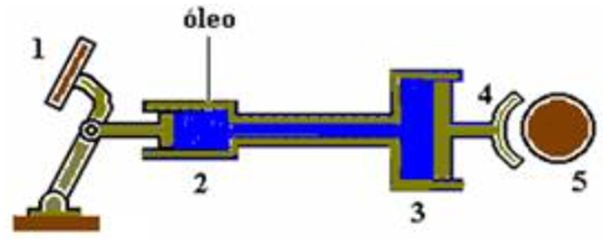
Determine se o freio é uma máquina que amplia deslocamento ou
força. Justifique.
Resolução:
Força. A força que age na roda é muito maior do que aquela
aplicada no pedal (Princípio de Pascal), devido à diferença de área entre os
êmbolos e também devido ao sistema de alavancas do pedal do freio.
25 - (CFT-MG) Analise a situação a seguir
representada.

O aumento de pressão em todas as partes do fluido
armazenado no recipiente está relacionado ao princípio de
a) Pascal.
b) Newton. c) Torricelli. d) Arquimedes.
Resolução:
A situação descrita no problema menciona o aumento
de pressão em todas as partes do fluido. Este fenômeno é explicado pelo
princípio de Pascal, onde a pressão é transmitida uniformemente.
Resposta: Letra A
26 - (UEG - 2011) Em uma colisão automobilística frontal, observou-se que o volante foi deformado provavelmente pelo impacto com o tórax do motorista, além de uma quebra circular no para-brisa evidenciar o local de impacto da cabeça. O acidentado apresentou fratura craniana, deformidade transversal do esterno, contusão cardíaca e ruptura dos alvéolos pulmonares. A lesão pulmonar ocorreu pela reação instintiva de espanto do motorista ao puxar e segurar o fôlego, pois a compressão súbita do tórax produziu a ruptura dos alvéolos, assim como se estoura um saco de papel inflado. Sobre essa lesão pulmonar, é CORRETO afirmar:
a) pelo Princípio de Pascal, o
aumento da pressão sobre o ar contido nos alvéolos foi inversamente
proporcional ao volume ocupado pelo fluido, cuja massa rompeu as paredes
inferiores dos alvéolos.
b) pelo Princípio de Pascal, o
aumento da pressão anteroposterior sobre o ar contido nos alvéolos por ação de
pressão externa foi transmitido a todos os pontos do fluido, inclusive à parede
dos alvéolos.
c) pelo Princípio de Arquimedes,
o aumento da pressão sobre o ar contido nos alvéolos foi inversamente
proporcional ao volume ocupado pelo fluido, cuja massa rompeu as paredes
inferiores dos alvéolos.
d) pelo Princípio de Arquimedes,
o aumento da pressão anteroposterior sobre o ar contido nos alvéolos por ação
de pressão externa foi transmitido a todos os pontos do fluido, inclusive à
parede dos alvéolos.
Resolução:
A situação descrita no problema menciona o aumento
de pressão em todas as partes do fluido. Este fenômeno é explicado pelo
princípio de Pascal, onde a pressão é transmitida uniformemente.
Resposta: Letra A
27 - (UFMG-MG) Um sistema hidráulico tem três êmbolos móveis
L, M e N com área A, 2A e 3A, como mostra a figura.
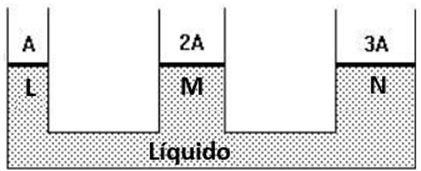
Quantidades diferentes de blocos são colocadas sobre cada êmbolo. Todos os blocos têm o mesmo peso. Para que, em equilíbrio, os êmbolos continuem na mesma altura, o número de blocos colocados sobre os êmbolos L, M e N podem ser, respectivamente:
a) 1, 2 e
3
b) 1, 4 e
9
c) 3, 2 e
1
d) 9, 4 e
1
e) 8, 2 e 1
Resolução:
A pressão exercida num fluido incompressível em equilíbrio se
transmite igualmente em todas as direções.
A pressão é definida como a força por unidade de área (P =
F/A). A força é a pressão multiplicada pela área (F = P ⋅ A).
Para que os êmbolos estejam em equilíbrio, a força exercida por
cada um deles deve ser a mesma.
Como a pressão é a mesma em todos os êmbolos, a força exercida por
cada um é diretamente proporcional à sua área.
Como todos os blocos têm o mesmo peso, a força que cada êmbolo
exerce é proporcional ao número de blocos que ele suporta.
Para que a força seja a mesma em todos os êmbolos, o número de
blocos deve ser proporcional à área. Portanto, para os êmbolos com áreas
A, 2A e 3A, o número de blocos deve ser 1, 2 e 3, respectivamente.
Resposta: Letra A






