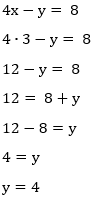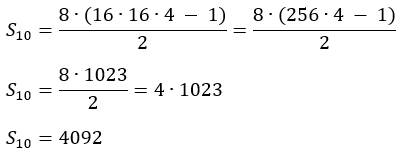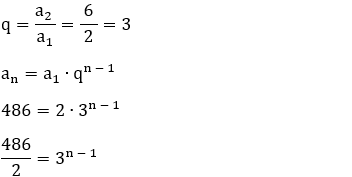Matrizes

1 - Escrever a matriz A, sendo: 

Resolução:

A matriz 2X3 será do tipo:

Calculado os valores dos elementos dessa matriz:

Logo:

2 – Dadas as matrizes A e B, sendo:

Calcular:

a) A + B^t              b)  A + 2B         c) A・B

Resolução:

a)

b)

c)

3 - Sejam as matrizes A, B e C:

O valor de A + B⋅C é:

Resolução:

4 – Calcule os valores de x e y, sabendo que:

Resolução:

Com isto vamos ter:

Somando as duas equações:

Substituindo o valor de x na primeira equação:

Solução: x = 3 e y = 4

Com isto vamos ter:

Resolvendo o sistema de equações:

Isolando x na equação (1):

Substituindo (3) em (2):

Substituindo o valor de y em (1):

Resposta: x = 4 e y = – 2

Soma dos termos de uma PG finita

Uma progressão geométrica (PG) é uma sequência numérica onde cada termo (exceto o primeiro) é obtido multiplicando o termo anterior por uma constante chamada razão. Exemplo: 2, 6, 18, 54... aqui, a razão é 3. Para uma PG finita, sabemos que ela possui um número limitado de termos.

A fórmula para a soma de uma PG finita é:

Onde:

·        Sn é a soma dos n primeiros termos da PG.

·        a₁ é o primeiro termo da sequência.

·        q é a razão.

·        n é o número de termos.

Exemplos

1 - Calcular a soma dos 5 primeiros termos da P. G. (9, 27, ...).

Resolução:

2 - Calcule a soma da P. G. (2, 8, ... , 2048).

Resolução:

• Vamos calcular o número de termos da PG:

• Bases iguais, expoentes iguais:

• Substituindo esses valores na equação:

Exercícios

1 – Qual é o valor da soma dos 10 primeiros termos da PG (3,6,12, 24, …)?

2 – Seja uma PG na qual o 1º termo é 2, o último é 256 e a soma dos termos é 510. Qual é o valor da razão dessa PG?

3 – Qual será a soma dos 10 primeiros termos da P. G. onde o primeiro termo é 8 e a razão 2?

4 – Calcule a soma da P. G. (2, 6, ... 486).

5 – Calcular a soma dos 8 primeiros termos da P. G. (8, 16, ...).

6 – Resolva a equação x + 2x + ... + 128x = 765, sabendo-se que os termos do 1º membro formam uma P. G.

7 – Resolva a equação x + 3x + ... + 81x = 1210, sabendo que os termos do 1º membro formam uma PG.

8 - Calcule a soma dos 6 primeiros termos da PG (6, 12, ... ).

Respostas:

1) Resolução:

2) Resolução:

• Substituindo os valores conhecidos em:

• Substituindo a equação (1) em (2):

3) Resolução:

Fazendo n = 10 na fórmula:

4) Resolução:

Dados:

Vamos calcular o número de termos da PG:

Substituindo esses valores na expressão:

5) Resolução:

Dados:

6) Resolução:

Dados:

Calculo de n:

Fatorando o número 128:

n = 7 + 1 ⇒   n = 8    

Substituindo o valor de n na expressão:

Solução: S = {3}

7) Resolução:

Dados:

Calculo de n:

n = 4 + 1 ⇒   n = 5    

Substituindo o valor de n na expressão:

Solução: S = {10}

8) Resolução: