Uma equação que pode ser escrita na forma reduzida ax² + bx + c = 0 é chamada de equação do 2° grau.
Se b = 0: ax² + c = 0
Se c = 0: ax² + bx = 0
As equações do 2° grau podem ter até duas soluções, que são chamados de raízes da equação. Para resolvermos equações do 2° grau, podemos usar a fórmula de Bhaskara:

Δ > 0 (duas raízes reais e distintas)
Δ = 0 (uma raiz real dupla)
Δ < 0 (Não tem raízes reais: duas raízes complexas)
De forma simplificada, podemos escrever a fórmula de Bhaskara:

Forma fatorada da equação da equação do 2º grau
ax2 + bx + c = 0 ou a⋅(x – x1)⋅(x – x2) = 0
Onde x1 e x2 são raízes da equação.

Exemplos
1 - Qual é a equação do 2º grau que tem raízes – 3 e 2 com o coeficiente a igual a 5?
Resolução:
a⋅(x –
x1)⋅(x –
x2) = 0
5⋅(x – (– 3))⋅( x – 2) = 0
5⋅(x + 3)⋅( x – 2) = 0
5⋅(x2 –
2x + 3x – 6) = 0
5⋅(x2 + x
– 6) = 0
5x2 + 5x – 30 = 0 :(5)
x2 + x – 6 = 0
2 – Simplifique a expressão:
Resolução:

3 – O valor do produto das raízes da equação
4x2 + 8x –
12 = 0 é:
a) – 12
b) 8
c) 2
d) – 3
e) não existe
Resolução:
a = 4, b = 8 e c = – 12

Resolução:
(x + 9)2 = 49

x + 9 = 7 ⇒ x = 7 – 9 ∴ x = – 2
ou
x + 9 = – 7 ⇒ x = – 7 – 9 ∴ x = – 16
Solução: {– 16, – 2}
Exercícios
4 - Resolva as equações de 2º grau:
c) x² + 4x – 5 = 0
d) x² – 10x + 24 = 0
e) 2x² – 9x + 4 = 0
f) x² + 8x + 16 = 0
7 – Resolva a equação do 2º grau x² – 37x + 300 = 0.

11 – Se (ax + 2) ⋅ (bx + 3) = 14x2 + cx + 6, para todos os valores de x e a + b = 9, quais são os dois possíveis valores de c?
a) 2 e 7 b) 4 e 14 c) 6 e 21 d) 20 e 25
Respostas:
Calculando o valor do discriminante Δ(Delta):
Δ = b² – 4⋅a⋅c
Como Δ > 0, a equação terá duas raízes. Substituindo o valor de Δ por 25:
e
Como Δ > 0, a equação terá duas raízes.
x = 8 – 8 = 0 = 0
Soluções: x = 0 e x = 4.
Como Δ < 0, a equação não possui raízes reais.

a = 1, b = 10 e c = 25












6 - Resolução:





Primeiramente vamos calcular as raízes da equação 2x² – 5x – 1 = 0, usando a fórmula de Bhaskara:












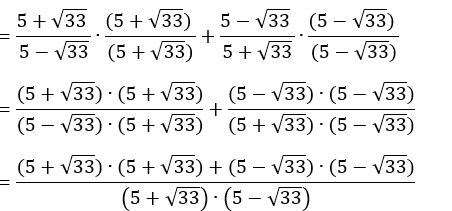





a = 1, b = – 9 e c = 8


10 – Resolução:
x² + 11x + 30 = 0
a = 1, b = 11 e c = 30


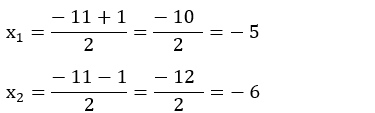
(ax + 2) ⋅ (bx + 3) = 14x2 + cx + 6
abx2 + 3ax + 2bx + 6 = 14x2 + cx + 6
abx2 + (3a + 2b)x + 6 = 14x2 + cx + 6
Comparando as igualdades:
ab = 14 (1)
3a + 2b = c (2)
a + b = 9 ⇒ a = 9 – b (3)
Substituindo (3) em (1):
(9 – b) ⋅b = 14
9b – b2 = 14
– b2 + 9b – 14 = 0 x(– 1)
b2 – 9b + 14 = 0
Usando a fórmula de Bhaskara:
A = 1, B = – 9 e C = 14
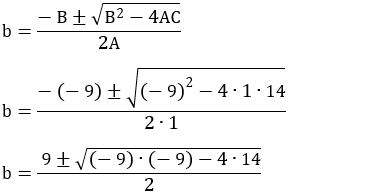

Substituindo b em (1):
a = 9 – b (3)
a1 = 9 – 7 = 2
a2 = 9 – 2 = 7
Substituindo a e b em (2):
3a + 2b = c (2)
Substituindo b em (1):
3a + 2b = c
c1 = 3⋅2 + 2⋅7 = 6 + 14 = 20
c2 = 3⋅7 + 2⋅2 = 21 + 4 = 25
Resposta: Letra D




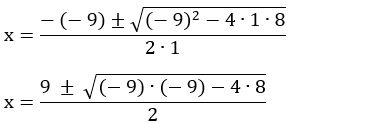
Nenhum comentário:
Postar um comentário