1 - Dada a progressão
aritmética (4, 8, 12, 16, …), calcule a soma dos seus 110 primeiros termos.
Resolução:
Primeiramente vamos
calcular o valor do 110° termo:

2 - Calcule a soma dos 50 primeiros termos da progressão aritmética (4, 8, 12, 16, …)
Resolução:
Primeiramente vamos calcular o
termo a50 dessa
progressão aritmética:
Fazendo n = 50 na fórmula da soma:


Resolução:
Primeiramente vamos
calcular o valor do 15° termo:

Cálculo da soma dos seus 15 primeiros termos:
 |

4 - Qual é a soma de todos os números de dois algarismos que têm resto 2 quando dividido por 3?
a) 3270
b) 2645
c) 2160
d) 1635
Resolução:
Vamos encontrar os primeiros menores números de dois algarismos que têm resto 2 quando divididos por 3:

11, 14, 17, ..., 98.

5 - Joana comprou um celular e dividiu
o pagamento em 24 parcelas mensais que formam uma progressão aritmética
crescente. As três primeiras parcelas foram de R$ 120,00, R$ 126,00 e R$
132,00. Sabendo que, ao final, constatou-se que Joana não pagou a 19ª parcela,
o valor pago por ela foi:
a)
R$ 3.954,00
b) R$ 4.026,00
c) R$ 4.200,00
d) R$ 4.308,00
e) R$ 4.382,00




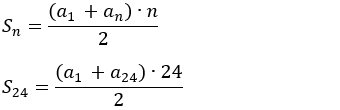

Valor pago:


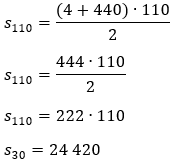




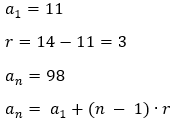










 Ângulos opostos pelo vértice
Ângulos opostos pelo vértice