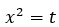1 - Quando eu nasci, meu pai tinha 32 anos. Hoje, o produto das nossas idades é 900. A soma das nossas idades atuais é igual a:
a) 72
b) 68
c) 64
d) 83
Resolução:
Nossas idades quando eu nasci:
Eu: 0
Meu pai: 32
Nossas idades atuais:
Eu: x
Meu pai: x + 32
Equação: x ⋅ (x + 32) = 900
Então, nossas idades atuais são:
Eu: x = 18 anos
Meu pai: x + 32 = 18 + 32 = 50 anos
Eu: x = 18 anos
Meu pai: x + 32 = 18 + 32 = 50 anos
Soma das idades: 18 anos + 50 anos = 68 anos
Resposta: A soma das nossas idades é de 68 anos.: 18 anos + 50 anos = 68 anos
2 - Daqui a 24 anos minha idade será o quadrado da idade que eu tinha a 18 anos atrás. Qual é minha idade hoje?
a) 22 anos
b) 23 anos
c) 24 anos
d) 25 anos
b) 23 anos
c) 24 anos
d) 25 anos
Resolução:
Minha idade hoje: x
Minha daqui a 24 anos: x + 24
O quadrado da idade que eu tinha a 18 anos atrás: (x – 18)²
Equação:
x + 24 = (x – 18)²
x + 24 = (x – 18)(x – 18)
x + 24 = x ⋅ x – x ⋅ 18 – 18 ⋅ x + 18 ⋅ 18
x + 24 = x² – 18x – 18x + 324
x + 24 = x² – 36x + 324
0 = x² – 36x – x + 324 – 24
Resposta: A minha idade hoje é 25 anos.
3 - O triplo de um número positivo somado com seu quadrado é igual a 180. Qual é esse número?
a) 15 b) 14 c) 13 d) 12
Resolução:
3x + x2 = 180
x2 + 3x ー180 = 0
Resposta: a
4 - A hipotenusa de um triângulo retângulo, representado abaixo, mede 10 m. A área desse triângulo é 24 m2. Quais as medidas dos catetos desse triângulo?
Resolução:
Pelo teorema de Pitágoras temos:
a² = b² + c²
10² = x² + y²
10 ⋅ 10 = x² + y²
x² + y² = 100
A área do triângulo é dada por:
Agora vamos resolver o sistema de equações:
Isolando y em (1):
Substituindo (3) em (2):
x² + y² = 100
Fazendo:
Multiplicando toda equação por t:
Como:
e
Então, as medidas de um dos lados medem x = 6 m ou x = 8 m (As medidas dos lados não podem ser negativas).
Cálculo das medidas de y:
Para x = 6
Para x = 8
Resposta: As medidas dos catetos são: 6 m e 8 m.
