Calcular o m.m.c. de dois ou mais números é o mesmo que encontrar o menor múltiplo comum entre os números. Múltiplos de um número natural é o produto da multiplicação desse número por outro, por exemplo:
Os múltiplos de 2 são:
2X0 = 0
2X1 = 2
2X2 = 4
2X3 = 6
2X4 = 8
2X5 = 10
2X6 = 12
.
.
.
Escrevemos: M(2) = {0, 2, 4, 6, 8, 10, 12, ...}
Os múltiplos de 3 são:
3X0 = 0
3X1 = 3
3X2 = 6
3X3 = 9
3X4 = 12
3X5 = 15
3X6 = 18
.
.
.
Escrevemos: M(3) = {0, 3, 6, 9, 12, 15, 18, ...}
Como o número zero é múltiplo de qualquer número, quando calculamos o m.m.c. de dois ou mais números, excluímos o zero:
Veja os exemplos:
1 – Qual é o mínimo múltiplo comum dos números 6 e 9?
Resolução:
M (6) = {0, 6, 12, (18), 24, 36, 42, 48, ...}
M (9) = {0, 9, (18), 27, 36, 45, 54, 63, ...}
m. m. c (6, 9) = 18
2 – Obtenha os oito primeiros múltiplos de 6, 9 e 12. Depois determine:
a) m. m. c (9,12);
Resolução:
M (9) = {0, 9, 18, 27, (36), 45, 54, 63, ...}
M (12) = {0, 12, 24, (36), 48, 60, 72, 84, ...}
m. m. c (9,12) = 36
b) m. m. c (6,12);
Resolução:
M (6) = {0, 6, (12), 18, 24, 36, 42, 48, ...}
M (12) = {0, (12), 24, 36, 48, 60, 72, 84, ...}
m. m. c (6,12) = 12
c) m. m. c (6,9,12).
Resolução:
M (6) = {0, 6, 12, 18, 24, (36), 42, 48, ...}
M (9) = {0, 9, 18, 27, (36), 45, 54, 63, ...}
M (12) = {0, 12, 24, (36), 48, 60, 72, 84, ...}
m. m. c (6,9,12) = 36
• Podemos também calcular o mínimo múltiplo comum de dois ou mais números por decomposição simultânea desses números:
3 – Qual é o mínimo múltiplo comum entre os números 4 e 5?
Resolução:
Resposta: m.m.c.(4, 5) = 20
4 – Calcular o mínimo múltiplo comum dos números 2, 3 e 4:
Resolução:
Resposta: m.m.c.(2, 3, 4) =12
5 – Determine o m.m.c. de 6,12 e 24.
Resolução:
Decompondo simultaneamente esses números, vamos encontrar:
Resposta: m.m.c. (6,12,24) = 24
6 – Encontre o m.m.c. de 6, 12, 24, 48.
Resolução:
Decompondo simultaneamente esses números, vamos encontrar:

Resposta: m.m.c. (6,12,24,48) = 48
7 – Calcule o mínimo múltiplo comum dos números 20, 24 e 30.
Resolução:
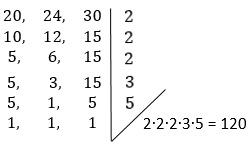
Resposta: 120
8 – Calcule o mínimo múltiplo comum dos números 15, 25 e 40.
Resolução:
Resposta: 600
9 – Qual é o mínimo múltiplo comum de 625 e 25?Resolução:
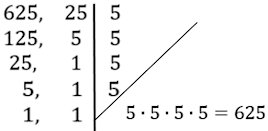
Resposta: m.m.c. (625,25) = 625
10 – Determine o m.m.c. dos números 18, 24 e 30.
Resolução:

Resposta: m.m.c. (18, 24, 30) = 360
11 – Determine:
a) m.m.c.(6, 15)
b) m.m.c.(7, 8)
c) m.m.c.(12, 15, 17)
Resolução:
a)

Resposta: m.m.c.(6, 15) = 30
b)

Resposta: m.m.c.(7, 8) = 56
c)

Resposta: m.m.c.(12, 15, 17) = 1020
12 – Uma empresa produz
cadarços de diferentes tamanhos 35 centímetros de 45 centímetros de 60 cm. Ela
compra de um fornecedor o fio para o cadarço menor comprimento possível possa
ser cortado em todos os tamanhos que serão comercializados. Qual é o comprimento
desse fio?
Resolução:
Para determinar o menor comprimento possível do fio que pode
ser cortado exatamente nos tamanhos de 35 cm, 45 cm e 60 cm, devemos encontrar
o mínimo múltiplo comum (MMC) desses números.
Resposta:
O menor comprimento possível do fio é 1260 cm (ou 12,6
metros).
Isso garante que o fio possa ser cortado exatamente em
segmentos de 35 cm, 45 cm e 60 cm sem sobra ou desperdício.















