O conjunto dos números reais (
Os números naturais são (0, 1, 2, 3, 4, 5 …) e assim por diante. Os inteiros incluem os números negativos (…–3, – 2, –1, 0, 1, 2, 3 …). Os racionais são aqueles que podem ser expressos na forma de fração 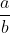 , em que "a" e "b" são números inteiros e "b" é diferente de 0 (4, -10, 1/2, 3/4, – 5/4, 0,25 etc.). Os irracionais são os que não podem ser obtidos pela divisão de dois números inteiros (
, em que "a" e "b" são números inteiros e "b" é diferente de 0 (4, -10, 1/2, 3/4, – 5/4, 0,25 etc.). Os irracionais são os que não podem ser obtidos pela divisão de dois números inteiros (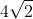 , –
, – 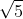 ,
,  , ou
, ou  = 3,141592 …, entre muitos outros).
= 3,141592 …, entre muitos outros).
Observe que:
1) Todo número natural é inteiro;
2) Todo número inteiro também é racional, embora não seja representado sob a forma de fração. Isso significa que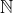 está contido em
está contido em 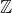 e que
e que 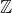 está contido em
está contido em 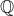 . Consequentemente,
. Consequentemente,  =
= 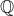
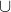
 .
.
1) Todo número natural é inteiro;
2) Todo número inteiro também é racional, embora não seja representado sob a forma de fração. Isso significa que
Um número irracional importante:
A razão entre a medida do comprimento(C) de uma circunferência e a medida do seu diâmetro(D) obtemos uma constante: o número pi; representado pela letra grega  .
.
 .
.1 - O número racional 1/6 é igual a:
a) 1,6
a) 1,6
b) 0,6
c) 0,16
d) 0,1666...
c) 0,16
d) 0,1666...
Resposta:
Como fração é divisão
1/6 = 1: 6 = 0,1666...
2 - O número 0,212121… é equivalente a:
a) 110/9
b) 21/99
a) 110/9
b) 21/99
c) 220/9
d) 9/22
d) 9/22
Resposta: Para encontrar a fração geratriz dessa dízima periódica, vamos fazer:
x = 0,212121...
Multiplicar por 100 ambos os lados dessa igualdade:
x = 0,212121... X 100
100x = 21,212121...
Subtraindo 100x - x vamos ter:
3 - O valor da expressão é:
A resposta correta é:
Resposta:






Nenhum comentário:
Postar um comentário